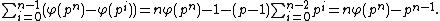Conductor-discriminant formula
Encyclopedia
In mathematics
, the conductor-discriminant formula is a formula calculating the discriminant
of a finite Galois extension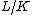
of global field
s from the global Artin conductors of the irreducible characters
of the Galois group
.
be a finite Galois extension of global fields with Galois group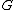 
. Then the discriminant
equals
where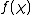
equals the global Artin conductor of 
.
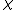be a cyclotomic extension
of the rationals. The Galois group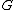
equals 
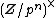. Because 
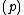is the only finite prime ramified, the global Artin conductor 
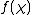equals the local one 
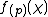. Because 
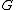is abelian, every non-trivial irreducible character 
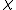is of degree 
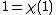. Then, the local Artin conductor of 
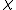equals the conductor of the 
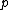-adic completion of 
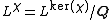, i.e. 
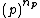, where 
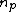is the smallest natural number such that 
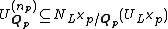. If 
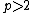, the Galois group 
is cyclic of order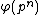 
, and by local class field theory and using that 
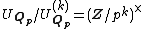one sees easily that 
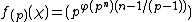: the exponent is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the conductor-discriminant formula is a formula calculating the discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of a finite Galois extension
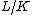of global fieldGlobal field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s from the global Artin conductors of the irreducible characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of the Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
.Statement
Let be a finite Galois extension of global fields with Galois group 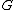. Then the discriminantDiscriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
equals
where
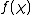equals the global Artin conductor of 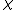.Example
Let be a cyclotomic extensionCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
of the rationals. The Galois group
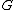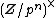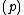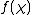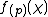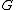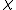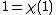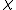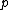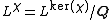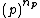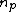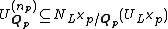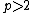equals . Because is the only finite prime ramified, the global Artin conductor equals the local one . Because is abelian, every non-trivial irreducible character is of degree . Then, the local Artin conductor of equals the conductor of the -adic completion of , i.e. , where is the smallest natural number such that . If , the Galois group is cyclic of order 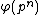, and by local class field theory and using that 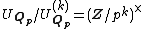one sees easily that 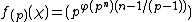: the exponent is