
Conjugate beam method
Encyclopedia
The conjugate-beam method is an engineering method to derive the slope and displacement of a beam. The conjugate-beam method was developed by H. Müller-Breslau in 1865. Essentially, it requires the same amount of computation as the moment-area theorems to determine a beam's slope or deflection; however, this method relies only on the principles of statics, so its application will be more familiar.
The basis for the method comes from the similarity of Eq. 1 and Eq 2 to Eq 3 and Eq 4. To show this similarity, these equations are shown below.
Integrated, the equations look like this.
Here the shear
V compares with the slope
θ, the moment
M compares with the displacement
v, and the external load w compares with the M/EI diagram. Below is a shear, moment, and deflection diagram. A M/EI diagram is a moment diagram divided my the beam's Young's modulus
and moment of inertia
.
To make use of this comparison we will now consider a beam having the same length as the real beam, but referred here as the "conjugate beam." The conjugate beam is "loaded" with the M/EI diagram derived from the load on the real beam. From the above comparisons, we can state two theorems related to the conjugate beam:
Theorem 1: The slope at a point tn the real beam is numerically equal to the shear at the corresponding point in the conjugate beam.
Theorem 2: The displacement of a point in the real beam is numerically equal to the moment at the corresponding point tn the conjugate beam.
real beams have unstable conjugate beams. Although this occurs, the M/EI loading will provide the necessary "equilibrium" to hold the conjugate beam stable.
and slope
at a point on the elastic curve of a beam using the conjugate-beam method.
The basis for the method comes from the similarity of Eq. 1 and Eq 2 to Eq 3 and Eq 4. To show this similarity, these equations are shown below.
 |
 |
 |
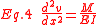 |
Integrated, the equations look like this.
 |
 |
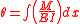 |
 |
Here the shear
Shear
Shear as a noun may refer to:*Bias , in clothing design, fabric may be cut on the shear*Cosmic shear, an effect of distortion of image of distant galaxies due to deflection of light by matter, as predicted by general relativity *Shear , a form of fault in rocks*Simple shear, a special case of...
V compares with the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
θ, the moment
Moment
- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
M compares with the displacement
Displacement
-Physics:*Displacement , the difference between the path of the initial and final position covered by a moving object**Particle displacement, a measurement of distance of the movement of a particle in a medium as it transmits a wave...
v, and the external load w compares with the M/EI diagram. Below is a shear, moment, and deflection diagram. A M/EI diagram is a moment diagram divided my the beam's Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
and moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
.
To make use of this comparison we will now consider a beam having the same length as the real beam, but referred here as the "conjugate beam." The conjugate beam is "loaded" with the M/EI diagram derived from the load on the real beam. From the above comparisons, we can state two theorems related to the conjugate beam:
Theorem 1: The slope at a point tn the real beam is numerically equal to the shear at the corresponding point in the conjugate beam.
Theorem 2: The displacement of a point in the real beam is numerically equal to the moment at the corresponding point tn the conjugate beam.
Conjugate-beam supports
When drawing the conjugate beam it is important that the shear and moment developed aththe supports of the conjugate beam account for the corresponding slope and displacement of the real beam at its supports, a consequence of Theorems 1 and 2. For example, as shown below, a pin or roller support at the end of the real beam provides zero displacement, but a non zero slope. Consequently, from Theorems 1 and 2, the conjugate beam must be supported by a pin or a roller, since this support has zero moment but has a shear or end reaction. When the real beam is fixed supported, both the slope and displacement are zero. Here the conjugate beam has a free end, since at this end there is zero shear and zero moment. Corresponding real and conjugate supports are shown below. Note that, as a rule, neglecting axial forces, statically determinate real beams have statically determinate conjugate beams; and statically indeterminateStatically indeterminate
In statics, a structure is statically indeterminate when the static equilibrium equations are insufficient for determining the internal forces and reactions on that structure....
real beams have unstable conjugate beams. Although this occurs, the M/EI loading will provide the necessary "equilibrium" to hold the conjugate beam stable.
| Real beam | Conjugate beam | ||
|---|---|---|---|
| Fixed support | Free end | ||
|
|
  |
||
| Free end | Fixed support | ||
 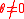 |
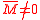 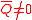 |
||
| Hinged support | Hinged support | ||
  |
 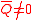 |
||
| Middle support | Middle hinge | ||
  :continue :continue |
  :continue :continue |
||
| Middle hinge | Middle support | ||
 :continue :continue :discontinue :discontinue |
 :continue :continue :discontinue :discontinue |
| Real beam | Conjugate beam | |
|---|---|---|
| Simple beam | ||
| Cantilever beam | ||
| Left-end Overhanging beam | ||
| Both-end overhanging beam | ||
| Gerber's beam (2 span) | ||
| Gerber's beam (3 span) |
Procedure for analysis
The following procedure provides a method that may be used to determine the displacementDisplacement
-Physics:*Displacement , the difference between the path of the initial and final position covered by a moving object**Particle displacement, a measurement of distance of the movement of a particle in a medium as it transmits a wave...
and slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
at a point on the elastic curve of a beam using the conjugate-beam method.
Conjugate beam
- Draw the conjugate beam for the real beam. This beam has the same length as the real beam and has corresponding supports as listed above.
- In general, if the real support allows a slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
, the conjugate support must develop shearShearShear as a noun may refer to:*Bias , in clothing design, fabric may be cut on the shear*Cosmic shear, an effect of distortion of image of distant galaxies due to deflection of light by matter, as predicted by general relativity *Shear , a form of fault in rocks*Simple shear, a special case of...
; and if the real support allows a displacementDisplacement-Physics:*Displacement , the difference between the path of the initial and final position covered by a moving object**Particle displacement, a measurement of distance of the movement of a particle in a medium as it transmits a wave...
, the conjugate support must develop a momentMoment- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
. - The conjugate beam is loaded with the real beam's M/EI diagram. This loading is assumed to be distributed over the conjugate beam and is directed upward when M/EI is positive and downward when M/EI is negative. In other words, the loading always acts away from the beam.
Equilibrium
- Using the equations of staticsStaticsStatics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
, determine the reactions at the conjugate beams supports. - Section the conjugate beam at the point where the slope θ and displacement Δ of the real beam are to be determined. At the section show the unknown shear V' and M' equal to θ and Δ, respectively, for the real beam. In particular, if these values are positive, and slope is counterclockwise and the displacement is upward.



