
Container (Type theory)
Encyclopedia
In type theory
, containers are abstractions which permit various "collection types", such as lists and trees
, to be represented in a uniform way. A (unary
) container is defined by a type of shapes S and a type family of positions P, indexed by S. The extension of a container is a family of dependent pairs consisting of a shape (of type S) and a function from positions of that shape to the element type. Containers can be seen as canonical form
s for collection types.
For lists, the shape type is the natural number
s (including zero). The corresponding position types are the types of natural numbers less than the shape, for each shape.
For trees, the shape type is the type of trees of units (that is, trees with no information in them, just structure). The corresponding position types are isomorphic to the types of valid paths from the root to particular nodes on the shape, for each shape.
Note that the natural numbers are isomorphic to lists of units. In general the shape type will always be isomorphic to the original non-generic container type family (list, tree etc.) applied to unit.
One of the main motivations for introducing the notion of containers is to support generic programming
in a dependently-typed setting.
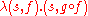
This is equivalent to the familiar
The element type (called the input type) is indexed by shape and position, so it can vary by shape and position, and the extension (called the output type) is also indexed by shape.
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, containers are abstractions which permit various "collection types", such as lists and trees
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
, to be represented in a uniform way. A (unary
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
) container is defined by a type of shapes S and a type family of positions P, indexed by S. The extension of a container is a family of dependent pairs consisting of a shape (of type S) and a function from positions of that shape to the element type. Containers can be seen as canonical form
Canonical form
Generally, in mathematics, a canonical form of an object is a standard way of presenting that object....
s for collection types.
For lists, the shape type is the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (including zero). The corresponding position types are the types of natural numbers less than the shape, for each shape.
For trees, the shape type is the type of trees of units (that is, trees with no information in them, just structure). The corresponding position types are isomorphic to the types of valid paths from the root to particular nodes on the shape, for each shape.
Note that the natural numbers are isomorphic to lists of units. In general the shape type will always be isomorphic to the original non-generic container type family (list, tree etc.) applied to unit.
One of the main motivations for introducing the notion of containers is to support generic programming
Generic programming
In a broad definition, generic programming is a style of computer programming in which algorithms are written in terms of to-be-specified-later types that are then instantiated when needed for specific types provided as parameters...
in a dependently-typed setting.
Categorical aspects
The extension of a container is an endofunctor. It takes a functiong to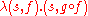
This is equivalent to the familiar
map g in the case of lists, and does something similar for other containers.Indexed containers
Indexed containers (also known as dependent polynomial functors) are a generalisation of containers, which can represent a wider class of types, such as vectors (sized lists).The element type (called the input type) is indexed by shape and position, so it can vary by shape and position, and the extension (called the output type) is also indexed by shape.

