Coplanarity
Encyclopedia
In geometry
, a set of points in space is coplanar if all the points lie in the same geometric plane
. For example, three distinct points are always coplanar; but a fourth point or more added in space can exist in another plane, incoplanarly.
Points can be shown to be coplanar by determining that the scalar product of a vector that is normal
to the plane and a vector from any point on the plane to the point being tested is 0. To put this another way, if you have a set of points which you want to determine are coplanar, first construct a vector for each point to one of the other points (by using the distance formula, for example). Secondly, construct a vector which is perpendicular
(normal) to the plane to test (for example, by computing the cross product
of two of the vectors from the first step). Finally, compute the dot product
(which is the same as the scalar product) of this vector with each of the vectors you created in the first step. If the result of each dot product is 0, then all the points are coplanar.
Distance geometry
provides a solution to the problem of determining if a set of points is coplanar, knowing only the distances between them.
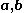and 
are coplanar, and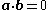 
, then
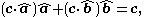
where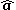
denotes the unit vector in the direction of 
.
Or, the vector resolutes of
on 
and 
on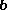 
add to give the original 
.
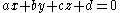, where 
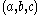is the normal vector of the plane.
The value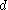
can be computed by plugging in one of the points and then solving. If 
is the same for all subsets of three points, then the planes are the same.
One advantage of this technique is that it can work in hyper-dimensional space. For example, suppose you wanted to compute the dihedral angle between two m-dimensional hyperplanes defined by m points in n-dimensional space. If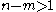
, then there are an infinite number of normal vectors for each hyperplane, so the angle between two of them is not necessarily the dihedral angle. However, if you use Gram-Schmidt process using the same initial vector in both cases, then the angle between the two normal vectors will be minimal, and therefore will be the dihedral angle between the hyperplanes.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a set of points in space is coplanar if all the points lie in the same geometric plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
. For example, three distinct points are always coplanar; but a fourth point or more added in space can exist in another plane, incoplanarly.
Points can be shown to be coplanar by determining that the scalar product of a vector that is normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the plane and a vector from any point on the plane to the point being tested is 0. To put this another way, if you have a set of points which you want to determine are coplanar, first construct a vector for each point to one of the other points (by using the distance formula, for example). Secondly, construct a vector which is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
(normal) to the plane to test (for example, by computing the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of two of the vectors from the first step). Finally, compute the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
(which is the same as the scalar product) of this vector with each of the vectors you created in the first step. If the result of each dot product is 0, then all the points are coplanar.
Distance geometry
Distance geometry
Distance geometry is the characterization and study of sets of points based only on given values of the distances between member pairs. Therefore distance geometry has immediate relevance where distance values are determined or considered, such as in surveying, cartography and...
provides a solution to the problem of determining if a set of points is coplanar, knowing only the distances between them.
Properties
If three vectors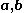 and are coplanar, and 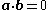, then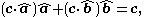where
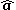denotes the unit vector in the direction of .Or, the vector resolutes of
on and on 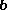add to give the original .Plane Formula
Another technique involves computing the formula for the planes defined by each subset of three points. First, the normal-vector for each plane is computed using some Orthogonalization technique. If the planes are parallel, then the dot-product of their normal-vectors will be 1 or -1. More specifically, the angle between the normal vectors can be computed. This is called the dihedral angle, and represents the smallest possible angle between the two planes. The formula for a plane is: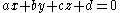, where 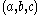is the normal vector of the plane.The value
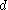can be computed by plugging in one of the points and then solving. If is the same for all subsets of three points, then the planes are the same.One advantage of this technique is that it can work in hyper-dimensional space. For example, suppose you wanted to compute the dihedral angle between two m-dimensional hyperplanes defined by m points in n-dimensional space. If
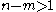, then there are an infinite number of normal vectors for each hyperplane, so the angle between two of them is not necessarily the dihedral angle. However, if you use Gram-Schmidt process using the same initial vector in both cases, then the angle between the two normal vectors will be minimal, and therefore will be the dihedral angle between the hyperplanes.