Corner detection
Encyclopedia
Corner detection is an approach used within computer vision
systems to extract certain kinds of features
and infer the contents of an image. Corner detection is frequently used in motion detection
, image registration
, video tracking
, image mosaicing
, panorama stitching, 3D modelling and object recognition
. Corner detection overlaps with the topic of interest point detection
.
An interest point is a point in an image which has a well-defined position and can be robustly detected. This means that an interest point can be a corner but it can also be, for example, an isolated point of local intensity maximum or minimum, line endings, or a point on a curve where the curvature is locally maximal.
In practice, most so-called corner detection methods detect interest points in general, rather than corners in particular. As a consequence, if only corners are to be detected it is necessary to do a local analysis of detected interest points to determine which of these are real corners. Examples of edge detection that can be used with post-processing to detect corners are the Kirsch-Operator
and the Frei-Chen masking set.
"Corner", "interest point" and "feature" are used interchangeably in literature, confusing the issue. Specifically, there are several blob detectors
that can be referred to as "interest point operators", but which are sometimes erroneously referred to as "corner detectors". Moreover, there exists a notion of ridge detection
to capture the presence of elongated objects.
Corner detectors are not usually very robust and often require expert supervision or large redundancies introduced to prevent the effect of individual errors from dominating the recognition task.
One determination of the quality of a corner detector is its ability to detect the same corner in multiple similar images, under conditions of different lighting, translation, rotation and other transforms.
A simple approach to corner detection in images is using correlation
, but this gets very computationally expensive and suboptimal. An alternative approach used frequently is based on a method proposed by Harris and Stephens (below), which in turn is an improvement of a method by Moravec.
If the pixel is in a region of uniform intensity, then the nearby patches will look similar. If the pixel is on an edge, then nearby patches in a direction perpendicular to the edge will look quite different, but nearby patches in a direction parallel to the edge will result only in a small change. If the pixel is on a feature with variation in all directions, then none of the nearby patches will look similar.
The corner strength is defined as the smallest SSD between the patch and its neighbors (horizontal, vertical and on the two diagonals). If this number is locally maximal, then a feature of interest is present.
As pointed out by Moravec, one of the main problems with this operator is that it is not isotropic: if an edge is present that is not in the direction of the neighbours, then it will not be detected as an interest point.
, since the term is used in the paper in which this detector is described. However, the mathematics in the paper clearly indicate that the sum of squared differences is used.)
Without loss of generality, we will assume a grayscale 2-dimensional image is used. Let this image be given by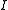
. Consider taking an image patch over the area 
and shifting it by 
. The weighted sum of squared differences (SSD) between these two patches, denoted 
, is given by:
can be approximated by a Taylor expansion
. Let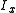
and 
be the partial derivatives of 
, such that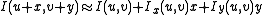
This produces the approximation
which can be written in matrix form: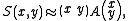
where A is the structure tensor
,
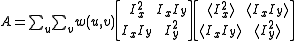
This matrix is a Harris matrix, and angle brackets denote averaging (i.e. summation over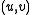
). If a circular window (or circularly weighted window, such as a Gaussian) is used, then the response will be isotropic.
A corner (or in general an interest point) is characterized by a large variation of
in all directions of the vector 
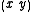. By analyzing the eigenvalues of 
, this characterization can be expressed in the following way: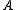 
should have two "large" eigenvalues for an interest point.
Based on the magnitudes of the eigenvalues, the following inferences can be made based on this argument:
Harris and Stephens note that exact computation of the eigenvalues is computationally expensive, since it requires the computation of a square root
, and instead suggest the
following function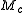
, where 
is a tunable sensitivity parameter:
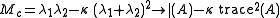
Therefore, the algorithm does not have to actually compute the eigenvalue decomposition of the matrix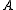
and
instead it is sufficient to evaluate the determinant
and trace
of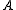
to find
corners, or rather interest points in general.
The Shi-Tomasi corner detector directly computes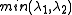
because under certain assumptions, the corners are more stable for tracking. Note that this method is also sometimes referred to as the Kanade-Tomasi corner detector.
The value of
has to be determined empirically, and in the literature values in the range 0.04 - 0.15 have been reported as feasible.
The covariance matrix
for the corner position is
, i.e.
)
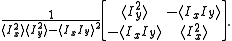
in the Harris operator, requires the computation of image derivatives 
in the image domain as well as the summation of non-linear combinations of these derivatives over local neighbourhoods. Since the computation of derivatives usually involves a stage of scale-space smoothing, an operational definition of the Harris operator requires two scale parameters: (i) a local scale for smoothing prior to the computation of image derivatives, and (ii) an integration scale for accumulating the non-linear operations on derivative operators into an integrated image descriptor.
With
denoting the original image intensity, let 
denote the scale-space representation of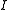 
obtained by convolution with a Gaussian kernel
with local scale parameter
:
and let
and 
denote the partial derivatives of 
.
Moreover, introduce a Gaussian window function
with integration scale parameter 
. Then, the multi-scale second-moment matrix can be defined as
Then, we can compute eigenvalues of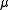
in a similar way as the eigenvalues of 
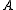and define the multi-scale Harris corner measure as
.
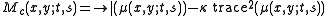Concerning the choice of the local scale parameter
and the integration scale parameter 
, these scale parameters are usually coupled by a relative integration scale parameter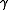 
such that 
, where 
is usually chosen in the interval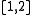 
. Thus, we can compute the multi-scale Harris corner measure 
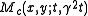at any scale 
in scale-space to obtain a multi-scale corner detector, which responds to corner structures of varying sizes in the image domain.
In practice, this multi-scale corner detector is often complemented by a scale selection step, where the scale-normalized Laplacian operator
is computed at every scale in scale-space and scale adapted corner points with automatic scale selection (the "Harris-Laplace operator") are computed from the points that are simultaneously:
of level curves and the gradient magnitude are simultaneously high.
A differential way to detect such points is by computing the rescaled level curve curvature (the product of the level curve curvature and the gradient magnitude raised to the power of three)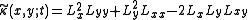
and to detect positive maxima and negative minima of this differential expression at some scale
in the scale-space representation 
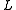of the original image.
A main problem with this approach, however, is that it may be sensitive to noise and to the choice of the scale level. A better method is to compute the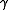
-normalized rescaled level curve curvature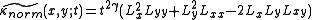
with
and to detect signed scale-space extrema of this expression, that are points and scales that are positive maxima and negative minima with respect to both space and scale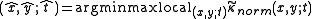
in combination with a complementary localization step to handle the increase in localization error at coarser scales. In this way, larger scale values will be associated with rounded corners of large spatial extent while smaller scale values will be associated with sharp corners with small spatial extent. This approach is the first corner detector with automatic scale selection (prior to the "Harris-Laplace operator" above) and has been used for tracking corners under large scale variations in the image domain.
These detectors are more completely described in blob detection
, however the LoG and DoG blobs do not necessarily make highly selective features, since these operators may also respond to edges. To improve the corner detection ability of the DoG detector, the feature detector used in the SIFT
system uses an additional post-processing stage, where the eigenvalues of the Hessian
of the image at the detection scale are examined in a similar way as in the Harris operator. If the ratio of the eigenvalues is too high, then the local image is regarded as too edge-like, so the feature is rejected. The DoH operator on the other hand only responds when there are significant grey-level variations in two directions.
where the shape of the smoothing kernel is iteratively warped to match the local image structure around the interest point or equivalently a local image patch is iteratively warped while the shape of the smoothing kernel remains rotationally symmetric. Hence, besides the commonly used multi-scale Harris operator, affine shape adaptation can be applied to other corner detectors as listed in this article as well as to differential blob detectors
such as the Laplacian/Difference of Gaussian operator, the determinant of the Hessian and the Hessian-Laplace operator.
along an image edge. In other words, the algorithm looks for places where the edge changes direction rapidly. The corner score,
, is given by:
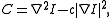
where
determines how edge-phobic the detector is. The authors also note that smoothing (Gaussian is suggested) is required to reduce noise. In this case, the first term of 
becomes the Laplacian (single-scale) blob detector
.
Smoothing also causes displacement of corners, so the authors derive an expression for the displacement of a 90 degree corner, and apply this as a correction factor to the detected corners.
For feature detection, SUSAN places a circular mask over the pixel to be tested (the nucleus). The region of the mask is
, and a pixel in this mask is represented by 
. The nucleus is at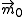 
. Every pixel is compared to the nucleus using the comparison function:
where
determines the radius, and the power of the exponent has been determined empirically. This function has the appearance of a smoothed top-hat or rectangular function. The area of the SUSAN is given by:
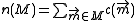
If
is the rectangular function, then 
is the number of pixels in the mask which are within 
of the nucleus. The response of the SUSAN operator is given by:
where
is named the `geometric threshold'. In other words the SUSAN operator only has a positive score if the area is small enough. The smallest SUSAN locally can be found using non-maximal suppression, and this is the complete SUSAN operator.
The value
determines how similar points have to be to the nucleus before they are considered to be part of the univalue segment. The value of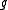 
determines the minimum size of the univalue segment. If 
is large enough, then this becomes an edge detector
.
For corner detection, two further steps are used. Firstly, the centroid
of the SUSAN is found. A proper corner will have the centroid far from the nucleus. The second step insists that all points on the line from the nucleus through the centroid out to the edge of the mask are in the SUSAN.
This technique is patented with UK patent 2272285.
is the pixel to be considered, and 
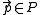is point on a circle 
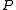centered around 
. The point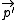 
is the point opposite to 
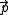along the diameter.
The response function is defined as:
This will be large when there is no direction in which the centre pixel is similar to two nearby pixels along a diameter.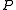
is a discretised circle (a Bresenham circle
), so interpolation
is used for intermediate diameters to give a more isotropic response. Since any computation gives an upper bound on the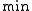
, the horizontal and vertical directions are checked first to see if it is worth proceeding with the complete computation of 
.
of radius
around the candidate point are considered. If 
contiguous pixels are all brighter than the nucleus by at least 
or all darker than the nucleus by 
, then the pixel under the nucleus is considered to be a feature. This test is reported to produce very stable features. The choice of the order in which the pixels are tested is a so called Twenty Questions problem
. Building short decision trees for this problem results in the most computationally efficient feature detectors available.
The first corner detection algorithm based on the AST is FAST (Features from Accelerated Segment Test). Although
can in principle take any value, FAST uses only a value of 3 (corresponding to a circle of 16 pixels circumference), and tests show that the best results are achieved with 
being 9. This value of 
is the lowest one at which edges are not detected. The order in which pixels are tested is determined by the ID3 algorithm
from a training set of images. Confusingly, the name of the detector is somewhat similar to the name of the paper describing Trajkovic and Hedley's detector.
is used to automatically synthesize image operators that can detect interest points. The terminal and function sets contain primitive operations that are common in many previously proposed man-made designs. Fitness
measures the stability of each operator through the repeatability rate, and promotes a uniform dispersion of detected points across the image plane. The performance of the evolved operators has been confirmed experimentally using training and testing sequences of progressively transformed images. Hence, the proposed GP algorithm is considered to be human-competitive for the problem of interest point detection.
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
systems to extract certain kinds of features
Feature detection
In computer vision and image processing the concept of feature detection refers to methods that aim at computing abstractions of image information and making local decisions at every image point whether there is an image feature of a given type at that point or not...
and infer the contents of an image. Corner detection is frequently used in motion detection
Motion detection
Motion detection is a process of confirming a change in position of an object relative to its surroundings or the change in the surroundings relative to an object. This detection can be achieved by both mechanical and electronic methods...
, image registration
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
, video tracking
Video tracking
Video tracking is the process of locating a moving object over time using a camera. It has a variety of uses, some of which are: human-computer interaction, security and surveillance, video communication and compression, augmented reality, traffic control, medical imaging and video editing...
, image mosaicing
Photographic mosaic
In the field of photographic imaging, a photographic mosaic, also known under the term Photomosaic, a portmanteau of photo and mosaic, is a picture that has been divided into rectangular sections, each of which is replaced with another photograph that matches the target photo...
, panorama stitching, 3D modelling and object recognition
Object recognition
Object recognition in computer vision is the task of finding a given object in an image or video sequence. Humans recognize a multitude of objects in images with little effort, despite the fact that the image of the objects may vary somewhat in different view points, in many different sizes / scale...
. Corner detection overlaps with the topic of interest point detection
Interest point detection
Interest point detection is a recent terminology in computer vision that refers to the detection of interest points for subsequent processing...
.
Formalization
A corner can be defined as the intersection of two edges. A corner can also be defined as a point for which there are two dominant and different edge directions in a local neighborhood of the point.An interest point is a point in an image which has a well-defined position and can be robustly detected. This means that an interest point can be a corner but it can also be, for example, an isolated point of local intensity maximum or minimum, line endings, or a point on a curve where the curvature is locally maximal.
In practice, most so-called corner detection methods detect interest points in general, rather than corners in particular. As a consequence, if only corners are to be detected it is necessary to do a local analysis of detected interest points to determine which of these are real corners. Examples of edge detection that can be used with post-processing to detect corners are the Kirsch-Operator
Kirsch-Operator
The Kirsch-operator is a non-linear edge detector that finds the maximum edge strength in a few predetermined directions.- Mathematical description :The operator is calculated as follows for directions with 45° difference:...
and the Frei-Chen masking set.
"Corner", "interest point" and "feature" are used interchangeably in literature, confusing the issue. Specifically, there are several blob detectors
Blob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
that can be referred to as "interest point operators", but which are sometimes erroneously referred to as "corner detectors". Moreover, there exists a notion of ridge detection
Ridge detection
The ridges of a smooth function of two variables is a set of curves whose points are, in one or more ways to be made precise below, local maxima of the function in at least one dimension. For a function of N variables, its ridges are a set of curves whose points are local maxima in N-1 dimensions...
to capture the presence of elongated objects.
Corner detectors are not usually very robust and often require expert supervision or large redundancies introduced to prevent the effect of individual errors from dominating the recognition task.
One determination of the quality of a corner detector is its ability to detect the same corner in multiple similar images, under conditions of different lighting, translation, rotation and other transforms.
A simple approach to corner detection in images is using correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, but this gets very computationally expensive and suboptimal. An alternative approach used frequently is based on a method proposed by Harris and Stephens (below), which in turn is an improvement of a method by Moravec.
The Moravec corner detection algorithm
This is one of the earliest corner detection algorithms and defines a corner to be a point with low self-similarity. The algorithm tests each pixel in the image to see if a corner is present, by considering how similar a patch centered on the pixel is to nearby, largely overlapping patches. The similarity is measured by taking the sum of squared differences (SSD) between the two patches. A lower number indicates more similarity.If the pixel is in a region of uniform intensity, then the nearby patches will look similar. If the pixel is on an edge, then nearby patches in a direction perpendicular to the edge will look quite different, but nearby patches in a direction parallel to the edge will result only in a small change. If the pixel is on a feature with variation in all directions, then none of the nearby patches will look similar.
The corner strength is defined as the smallest SSD between the patch and its neighbors (horizontal, vertical and on the two diagonals). If this number is locally maximal, then a feature of interest is present.
As pointed out by Moravec, one of the main problems with this operator is that it is not isotropic: if an edge is present that is not in the direction of the neighbours, then it will not be detected as an interest point.
The Harris & Stephens / Plessey / Shi-Tomasi corner detection algorithm
Harris and Stephens improved upon Moravec's corner detector by considering the differential of the corner score with respect to direction directly, instead of using shifted patches. (This corner score is often referred to as autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
, since the term is used in the paper in which this detector is described. However, the mathematics in the paper clearly indicate that the sum of squared differences is used.)
Without loss of generality, we will assume a grayscale 2-dimensional image is used. Let this image be given by
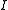. Consider taking an image patch over the area and shifting it by . The weighted sum of squared differences (SSD) between these two patches, denoted , is given by: can be approximated by a Taylor expansionTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. Let
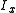and be the partial derivatives of , such that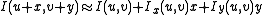This produces the approximation
which can be written in matrix form:
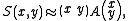
where A is the structure tensor
Structure tensor
In mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix derived from the gradient of a function. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent...
,
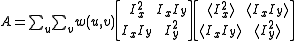
This matrix is a Harris matrix, and angle brackets denote averaging (i.e. summation over
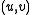). If a circular window (or circularly weighted window, such as a Gaussian) is used, then the response will be isotropic.A corner (or in general an interest point) is characterized by a large variation of
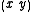in all directions of the vector . By analyzing the eigenvalues of , this characterization can be expressed in the following way: 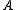should have two "large" eigenvalues for an interest point.Based on the magnitudes of the eigenvalues, the following inferences can be made based on this argument:
- If
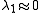and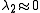 
then this pixel 
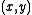has no features of interest. - If
and 
has some large positive value, then an edge is found. - If
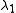and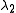 
have large positive values, then a corner is found.
Harris and Stephens note that exact computation of the eigenvalues is computationally expensive, since it requires the computation of a square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, and instead suggest the
following function
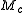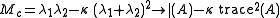
, where is a tunable sensitivity parameter:Therefore, the algorithm does not have to actually compute the eigenvalue decomposition of the matrix
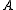andinstead it is sufficient to evaluate the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of
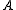to findcorners, or rather interest points in general.
The Shi-Tomasi corner detector directly computes
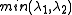because under certain assumptions, the corners are more stable for tracking. Note that this method is also sometimes referred to as the Kanade-Tomasi corner detector.The value of
has to be determined empirically, and in the literature values in the range 0.04 - 0.15 have been reported as feasible.The covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
for the corner position is
, i.e.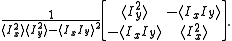The multi-scale Harris operator
The computation of the second moment matrix (sometimes also referred to as the structure tensorStructure tensor
In mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix derived from the gradient of a function. It summarizes the predominant directions of the gradient in a specified neighborhood of a point, and the degree to which those directions are coherent...
)
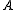in the Harris operator, requires the computation of image derivatives in the image domain as well as the summation of non-linear combinations of these derivatives over local neighbourhoods. Since the computation of derivatives usually involves a stage of scale-space smoothing, an operational definition of the Harris operator requires two scale parameters: (i) a local scale for smoothing prior to the computation of image derivatives, and (ii) an integration scale for accumulating the non-linear operations on derivative operators into an integrated image descriptor.With
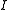denoting the original image intensity, let denote the scale-space representation of 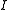obtained by convolution with a Gaussian kernelwith local scale parameter
:and let
and denote the partial derivatives of .Moreover, introduce a Gaussian window function
with integration scale parameter . Then, the multi-scale second-moment matrix can be defined asThen, we can compute eigenvalues of
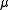in a similar way as the eigenvalues of 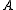and define the multi-scale Harris corner measure as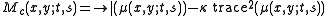.Concerning the choice of the local scale parameter
and the integration scale parameter , these scale parameters are usually coupled by a relative integration scale parameter 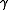such that , where is usually chosen in the interval 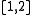. Thus, we can compute the multi-scale Harris corner measure 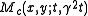at any scale in scale-space to obtain a multi-scale corner detector, which responds to corner structures of varying sizes in the image domain.In practice, this multi-scale corner detector is often complemented by a scale selection step, where the scale-normalized Laplacian operator
is computed at every scale in scale-space and scale adapted corner points with automatic scale selection (the "Harris-Laplace operator") are computed from the points that are simultaneously:
- spatial maxima of the multi-scale corner measure
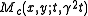
- local maxima or minima over scales of the scale-normalized Laplacian operator
.
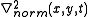
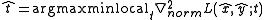The level curve curvature approach
An earlier approach to corner detection is to detect points where the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of level curves and the gradient magnitude are simultaneously high.
A differential way to detect such points is by computing the rescaled level curve curvature (the product of the level curve curvature and the gradient magnitude raised to the power of three)
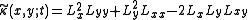
and to detect positive maxima and negative minima of this differential expression at some scale
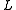in the scale-space representation of the original image.A main problem with this approach, however, is that it may be sensitive to noise and to the choice of the scale level. A better method is to compute the
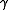-normalized rescaled level curve curvature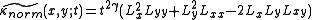with
and to detect signed scale-space extrema of this expression, that are points and scales that are positive maxima and negative minima with respect to both space and scale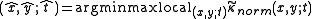in combination with a complementary localization step to handle the increase in localization error at coarser scales. In this way, larger scale values will be associated with rounded corners of large spatial extent while smaller scale values will be associated with sharp corners with small spatial extent. This approach is the first corner detector with automatic scale selection (prior to the "Harris-Laplace operator" above) and has been used for tracking corners under large scale variations in the image domain.
LoG, DoG, and DoH feature detection
LoG is an acronym standing for Laplacian of Gaussian, DoG is an acronym standing for Difference of Gaussians (DoG is an approximation of LoG), and DoH is an acronym standing for Determinant of the Hessian.These detectors are more completely described in blob detection
Blob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
, however the LoG and DoG blobs do not necessarily make highly selective features, since these operators may also respond to edges. To improve the corner detection ability of the DoG detector, the feature detector used in the SIFT
Scale-invariant feature transform
Scale-invariant feature transform is an algorithm in computer vision to detect and describe local features in images. The algorithm was published by David Lowe in 1999....
system uses an additional post-processing stage, where the eigenvalues of the Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of the image at the detection scale are examined in a similar way as in the Harris operator. If the ratio of the eigenvalues is too high, then the local image is regarded as too edge-like, so the feature is rejected. The DoH operator on the other hand only responds when there are significant grey-level variations in two directions.
Affine-adapted interest point operators
The interest points obtained from the multi-scale Harris operator with automatic scale selection are invariant to translations, rotations and uniform rescalings in the spatial domain. The images that constitute the input to a computer vision system are, however, also subject to perspective distortions. To obtain an interest point operator that is more robust to perspective transformations, a natural approach is to devise a feature detector that is invariant to affine transformations. In practice, affine invariant interest points can be obtained by applying affine shape adaptationAffine shape adaptation
Affine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...
where the shape of the smoothing kernel is iteratively warped to match the local image structure around the interest point or equivalently a local image patch is iteratively warped while the shape of the smoothing kernel remains rotationally symmetric. Hence, besides the commonly used multi-scale Harris operator, affine shape adaptation can be applied to other corner detectors as listed in this article as well as to differential blob detectors
Blob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
such as the Laplacian/Difference of Gaussian operator, the determinant of the Hessian and the Hessian-Laplace operator.
The Wang and Brady corner detection algorithm
The Wang and Brady detector considers the image to be a surface, and looks for places where there is large curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
along an image edge. In other words, the algorithm looks for places where the edge changes direction rapidly. The corner score,
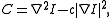
, is given by:where
determines how edge-phobic the detector is. The authors also note that smoothing (Gaussian is suggested) is required to reduce noise. In this case, the first term of becomes the Laplacian (single-scale) blob detectorBlob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
.
Smoothing also causes displacement of corners, so the authors derive an expression for the displacement of a 90 degree corner, and apply this as a correction factor to the detected corners.
The SUSAN corner detector
SUSAN is an acronym standing for Smallest Univalue Segment Assimilating Nucleus.For feature detection, SUSAN places a circular mask over the pixel to be tested (the nucleus). The region of the mask is
, and a pixel in this mask is represented by . The nucleus is at . Every pixel is compared to the nucleus using the comparison function:where
determines the radius, and the power of the exponent has been determined empirically. This function has the appearance of a smoothed top-hat or rectangular function. The area of the SUSAN is given by: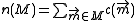If
is the rectangular function, then is the number of pixels in the mask which are within of the nucleus. The response of the SUSAN operator is given by:where
is named the `geometric threshold'. In other words the SUSAN operator only has a positive score if the area is small enough. The smallest SUSAN locally can be found using non-maximal suppression, and this is the complete SUSAN operator.The value
determines how similar points have to be to the nucleus before they are considered to be part of the univalue segment. The value of 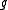determines the minimum size of the univalue segment. If is large enough, then this becomes an edge detectorEdge detection
Edge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
.
For corner detection, two further steps are used. Firstly, the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the SUSAN is found. A proper corner will have the centroid far from the nucleus. The second step insists that all points on the line from the nucleus through the centroid out to the edge of the mask are in the SUSAN.
This technique is patented with UK patent 2272285.
The Trajkovic and Hedley corner detector
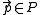In a manner similar to SUSAN, this detector directly tests whether a patch under a pixel is self-similar by examining nearby pixels. is the pixel to be considered, and is point on a circle 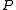centered around . The point 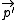is the point opposite to 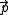along the diameter.The response function is defined as:
This will be large when there is no direction in which the centre pixel is similar to two nearby pixels along a diameter.
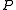is a discretised circle (a Bresenham circleMidpoint circle algorithm
In computer graphics, the midpoint circle algorithm is an algorithm used to determine the points needed for drawing a circle. The algorithm is a variant of Bresenham's line algorithm, and is thus sometimes known as Bresenham's circle algorithm, although not actually invented by Bresenham...
), so interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
is used for intermediate diameters to give a more isotropic response. Since any computation gives an upper bound on the
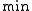, the horizontal and vertical directions are checked first to see if it is worth proceeding with the complete computation of .AST based feature detectors
AST is an acronym standing for Accelerated Segment Test. This test is a relaxed version of the SUSAN corner criterion. Instead of evaluating the circular disc only the pixels in a Bresenham circleMidpoint circle algorithm
In computer graphics, the midpoint circle algorithm is an algorithm used to determine the points needed for drawing a circle. The algorithm is a variant of Bresenham's line algorithm, and is thus sometimes known as Bresenham's circle algorithm, although not actually invented by Bresenham...
of radius
around the candidate point are considered. If contiguous pixels are all brighter than the nucleus by at least or all darker than the nucleus by , then the pixel under the nucleus is considered to be a feature. This test is reported to produce very stable features. The choice of the order in which the pixels are tested is a so called Twenty Questions problemTwenty Questions
Twenty Questions is a spoken parlor game which encourages deductive reasoning and creativity. It originated in the United States and escalated in popularity during the late 1940s when it became the format for a successful weekly radio quiz program....
. Building short decision trees for this problem results in the most computationally efficient feature detectors available.
The first corner detection algorithm based on the AST is FAST (Features from Accelerated Segment Test). Although
can in principle take any value, FAST uses only a value of 3 (corresponding to a circle of 16 pixels circumference), and tests show that the best results are achieved with being 9. This value of is the lowest one at which edges are not detected. The order in which pixels are tested is determined by the ID3 algorithmID3 algorithm
In decision tree learning, ID3 is an algorithm used to generate a decision tree invented by Ross Quinlan. ID3 is the precursor to the C4.5 algorithm.-Algorithm:The ID3 algorithm can be summarized as follows:...
from a training set of images. Confusingly, the name of the detector is somewhat similar to the name of the paper describing Trajkovic and Hedley's detector.
Automatic synthesis of detectors
Trujillo and Olague introduced a method by which genetic programmingGenetic programming
In artificial intelligence, genetic programming is an evolutionary algorithm-based methodology inspired by biological evolution to find computer programs that perform a user-defined task. It is a specialization of genetic algorithms where each individual is a computer program...
is used to automatically synthesize image operators that can detect interest points. The terminal and function sets contain primitive operations that are common in many previously proposed man-made designs. Fitness
Fitness function
A fitness function is a particular type of objective function that is used to summarise, as a single figure of merit, how close a given design solution is to achieving the set aims....
measures the stability of each operator through the repeatability rate, and promotes a uniform dispersion of detected points across the image plane. The performance of the evolved operators has been confirmed experimentally using training and testing sequences of progressively transformed images. Hence, the proposed GP algorithm is considered to be human-competitive for the problem of interest point detection.
Reference implementations
This section provides external links to reference implementations of some of the detectors described above. These reference implementations are provided by the authors of the paper in which the detector is first described. These may contain details not present or explicit in the papers describing the features.- DoG detection (as part of the SIFTScale-invariant feature transformScale-invariant feature transform is an algorithm in computer vision to detect and describe local features in images. The algorithm was published by David Lowe in 1999....
system), WindowsMicrosoft WindowsMicrosoft Windows is a series of operating systems produced by Microsoft.Microsoft introduced an operating environment named Windows on November 20, 1985 as an add-on to MS-DOS in response to the growing interest in graphical user interfaces . Microsoft Windows came to dominate the world's personal...
and x86 LinuxLinuxLinux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
executables - Harris-Laplace, static LinuxLinuxLinux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
executables. Also contains DoG and LoG detectors and affine adaptation for all detectors included. - FAST detector, C, C++, MATLAB source code and executables for various operating systems and architectures.
- lip-vireo,[LoG, DoG, Harris-Laplacian, Hessian and Hessian-Laplacian],[SIFT, flip invariant SIFT, PCA-SIFT, PSIFT, Steerable Filters, SPIN][Linux, Windows and SunOS] executables.
- FAST Detector for the iPhone, Adaptation of Edward Rosten's implementation to the iPhone. Achieves real time results.
See also
- blob detectionBlob detectionIn the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
- affine shape adaptationAffine shape adaptationAffine shape adaptation is a methodology for iteratively adapting the shape of the smoothing kernels in an affine group of smoothing kernels to the local image structure in neighbourhood region of a specific image point...
- scale-space
- ridge detectionRidge detectionThe ridges of a smooth function of two variables is a set of curves whose points are, in one or more ways to be made precise below, local maxima of the function in at least one dimension. For a function of N variables, its ridges are a set of curves whose points are local maxima in N-1 dimensions...
- interest point detectionInterest point detectionInterest point detection is a recent terminology in computer vision that refers to the detection of interest points for subsequent processing...
- feature detection (computer vision)
- Entry on corner detection in Encyclopedia of Mathematics