
Correlated equilibrium
Encyclopedia
In game theory
, a correlated equilibrium is a solution concept
that is more general than the well known Nash equilibrium
. It was first discussed by mathematician Robert Aumann
(1974). The idea is that each player chooses his/her action according to his/her observation of the value of the same public signal. A strategy assigns an action to every possible observation a player can make. If no player would want to deviate from the recommended strategy (assuming the others don't deviate), the distribution is called a correlated equilibrium.
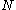 -player strategic game
-player strategic game 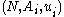 is characterized by an action set
is characterized by an action set 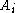 and utility function
and utility function 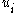 for each player
for each player 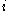 . When player
. When player 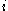 chooses strategy
chooses strategy  and the remaining players choose a strategy profile described by the
and the remaining players choose a strategy profile described by the  -tuple
-tuple 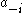 , then player
, then player 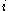 's utility is
's utility is 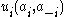 .
.
A "strategy modification" for player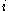 is a function
is a function 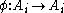 . That is,
. That is, 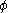 tells player
tells player 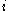 to modify his behavior by playing action
to modify his behavior by playing action 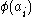 when instructed to play
when instructed to play 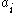 .
.
Let be a countable probability space
be a countable probability space
. For each player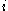 , let
, let 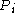 be his information partition,
be his information partition, 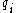 be
be  's posterior and let
's posterior and let 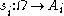 , assigning the same value to states in the same cell of
, assigning the same value to states in the same cell of 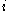 's information partition. Then
's information partition. Then  is a correlated equilibrium of the strategic game
is a correlated equilibrium of the strategic game  if for every player
if for every player 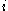 and for every strategy modification
and for every strategy modification 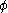 :
:
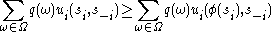
In other words,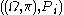 is a correlated equilibrium if no player can improve his expected utility via a strategy modification.
is a correlated equilibrium if no player can improve his expected utility via a strategy modification.
In this game, there are three Nash equilibria. The two pure strategy Nash equilibria are (D, C) and (C, D). There is also a mixed strategy equilibrium where each player Dares with probability 1/3.
Now consider a third party (or some natural event) that draws one of three cards labeled: (C, C), (D, C), and (C, D), with the same probability, i.e. probability 1/3 for each card. After drawing the card the third party informs the players of the strategy assigned to them on the card (but not the strategy assigned to their opponent). Suppose a player is assigned D, he would not want to deviate supposing the other player played their assigned strategy since he will get 7 (the highest payoff possible). Suppose a player is assigned C. Then the other player will play C with probability 1/2 and D with probability 1/2. The expected utility of Daring is 0(1/2) + 7(1/2) = 3.5 and the expected utility of chickening out is 2(1/2) + 6(1/2) = 4. So, the player would prefer to Chicken out.
Since neither player has an incentive to deviate, this is a correlated equilibrium. Interestingly, the expected payoff for this equilibrium is 7(1/3) + 2(1/3) + 6(1/3) = 5 which is higher than the expected payoff of the mixed strategy Nash equilibrium.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, a correlated equilibrium is a solution concept
Solution concept
In game theory, a solution concept is a formal rule for predicting how the game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players, therefore predicting the result of the game...
that is more general than the well known Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. It was first discussed by mathematician Robert Aumann
Robert Aumann
Robert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
(1974). The idea is that each player chooses his/her action according to his/her observation of the value of the same public signal. A strategy assigns an action to every possible observation a player can make. If no player would want to deviate from the recommended strategy (assuming the others don't deviate), the distribution is called a correlated equilibrium.
Formal definition
An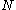 -player strategic game
-player strategic game 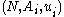 is characterized by an action set
is characterized by an action set 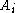 and utility function
and utility function 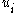 for each player
for each player 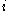 . When player
. When player 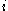 chooses strategy
chooses strategy  and the remaining players choose a strategy profile described by the
and the remaining players choose a strategy profile described by the  -tuple
-tuple 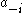 , then player
, then player 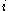 's utility is
's utility is 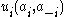 .
.A "strategy modification" for player
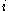 is a function
is a function 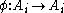 . That is,
. That is, 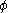 tells player
tells player 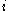 to modify his behavior by playing action
to modify his behavior by playing action 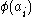 when instructed to play
when instructed to play 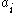 .
.Let
 be a countable probability space
be a countable probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. For each player
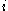 , let
, let 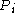 be his information partition,
be his information partition, 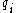 be
be  's posterior and let
's posterior and let 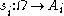 , assigning the same value to states in the same cell of
, assigning the same value to states in the same cell of 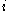 's information partition. Then
's information partition. Then  is a correlated equilibrium of the strategic game
is a correlated equilibrium of the strategic game  if for every player
if for every player 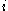 and for every strategy modification
and for every strategy modification 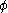 :
: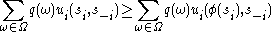
In other words,
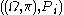 is a correlated equilibrium if no player can improve his expected utility via a strategy modification.
is a correlated equilibrium if no player can improve his expected utility via a strategy modification.An example
Consider the game of chicken pictured to the right. In this game two individuals are challenging each other to a contest where each can either dare or chicken out. If one is going to Dare, it is better for the other to chicken out. But if one is going to chicken out it is better for the other to Dare. This leads to an interesting situation where each wants to dare, but only if the other might chicken out.In this game, there are three Nash equilibria. The two pure strategy Nash equilibria are (D, C) and (C, D). There is also a mixed strategy equilibrium where each player Dares with probability 1/3.
Now consider a third party (or some natural event) that draws one of three cards labeled: (C, C), (D, C), and (C, D), with the same probability, i.e. probability 1/3 for each card. After drawing the card the third party informs the players of the strategy assigned to them on the card (but not the strategy assigned to their opponent). Suppose a player is assigned D, he would not want to deviate supposing the other player played their assigned strategy since he will get 7 (the highest payoff possible). Suppose a player is assigned C. Then the other player will play C with probability 1/2 and D with probability 1/2. The expected utility of Daring is 0(1/2) + 7(1/2) = 3.5 and the expected utility of chickening out is 2(1/2) + 6(1/2) = 4. So, the player would prefer to Chicken out.
Since neither player has an incentive to deviate, this is a correlated equilibrium. Interestingly, the expected payoff for this equilibrium is 7(1/3) + 2(1/3) + 6(1/3) = 5 which is higher than the expected payoff of the mixed strategy Nash equilibrium.

