Correlation clustering
Encyclopedia
In machine learning
, correlation clustering or cluster editing operates in a scenario where the relationship between the objects are known instead of the actual representation of the objects. For example, given a signed graph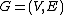
where the edge label indicates whether two nodes are similar (+) or different (−), the task is to cluster the vertices so that similar objects are grouped together. Unlike other clustering algorithms this does not require choosing the number of clusters
in advance because the objective, to minimize the disagreements, is independent of the number of clusters.
It may not be possible to find a perfect clustering, where all similar items are in a cluster while all dissimilar ones are in different clusters. If the graph indeed admits a perfect clustering, then simply deleting all the negative edges and finding the connected components in the remaining graph will return the required clusters.
But, in general a graph may not have a perfect clustering. For example, given nodes a,b,c such that a,b and a,c are similar while b,c are dissimilar, a perfect clustering is not possible. In such cases, the task is to find a clustering that maximizes the number of agreements (number of + edges inside clusters plus the number of - edges between clusters) or minimizes the number of disagreements (the number of - edges inside clusters plus the number of + edges between clusters). This problem of maximizing the agreements is NP-complete (multiway cut problem reduces to maximizing weighted agreements and the problem of partitioning into triangles can be reduced to unweighted version)
Bansal et al. discuss the NP-completeness proof and also present both a constant factor approximation algorithm and polynomial-time approximation scheme
to find the clusters in this setting. Ailon et al. propose a randomized 3-approximation algorithm for the same problem.
The authors show that the above algorithm is a 3-approximation algorithm for correlation clustering.
s among attributes of feature vector
s in a high-dimensional space are assumed to exist guiding the clustering process. These correlations may be different in different clusters, thus a global decorrelation
cannot reduce this to traditional (uncorrelated) clustering.
Correlations among subsets of attributes result in different spatial shapes of clusters. Hence, the similarity between cluster objects is defined by taking into account the local correlation patterns. With this notion, the term has been introduced in simultaneously with the notion discussed above.
Different methods for correlation clustering of this type are discussed in , the relationship to different types of clustering is discussed in , see also Clustering high-dimensional data
.
Correlation clustering (according to this definition) can be shown to be closely related to biclustering
. As in biclustering, the goal is to identify groups of objects that share a correlation in some of their attributes; where the correlation is usually typical for the individual clusters.
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, correlation clustering or cluster editing operates in a scenario where the relationship between the objects are known instead of the actual representation of the objects. For example, given a signed graph
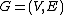where the edge label indicates whether two nodes are similar (+) or different (−), the task is to cluster the vertices so that similar objects are grouped together. Unlike other clustering algorithms this does not require choosing the number of clustersDetermining the number of clusters in a data set
Determining the number of clusters in a data set, a quantity often labeled k as in the k-means algorithm, is a frequent problem in data clustering, and is a distinct issue from the process of actually solving the clustering problem....
in advance because the objective, to minimize the disagreements, is independent of the number of clusters.It may not be possible to find a perfect clustering, where all similar items are in a cluster while all dissimilar ones are in different clusters. If the graph indeed admits a perfect clustering, then simply deleting all the negative edges and finding the connected components in the remaining graph will return the required clusters.
But, in general a graph may not have a perfect clustering. For example, given nodes a,b,c such that a,b and a,c are similar while b,c are dissimilar, a perfect clustering is not possible. In such cases, the task is to find a clustering that maximizes the number of agreements (number of + edges inside clusters plus the number of - edges between clusters) or minimizes the number of disagreements (the number of - edges inside clusters plus the number of + edges between clusters). This problem of maximizing the agreements is NP-complete (multiway cut problem reduces to maximizing weighted agreements and the problem of partitioning into triangles can be reduced to unweighted version)
Bansal et al. discuss the NP-completeness proof and also present both a constant factor approximation algorithm and polynomial-time approximation scheme
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
to find the clusters in this setting. Ailon et al. propose a randomized 3-approximation algorithm for the same problem.
CC-Pivot(G=(V,E+,E-))
Pick random pivot i ∈ V
Set 
, V'=Ø
For all j ∈ V, j ≠ i;
If (i,j) ∈ E+ then
Add j to C
Else (If (i,j) ∈ E-)
Add j to V'
Let G' be the subgraph induced by V'
Return clustering C,CC-Pivot(G')
The authors show that the above algorithm is a 3-approximation algorithm for correlation clustering.
Correlation clustering (data mining)
Correlation clustering also relates to a different task, where correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s among attributes of feature vector
Feature vector
In pattern recognition and machine learning, a feature vector is an n-dimensional vector of numerical features that represent some object. Many algorithms in machine learning require a numerical representation of objects, since such representations facilitate processing andstatistical analysis...
s in a high-dimensional space are assumed to exist guiding the clustering process. These correlations may be different in different clusters, thus a global decorrelation
Decorrelation
Decorrelation is a general term for any process that is used to reduce autocorrelation within a signal, or cross-correlation within a set of signals, while preserving other aspects of the signal. A frequently used method of decorrelation is the use of a matched linear filter to reduce the...
cannot reduce this to traditional (uncorrelated) clustering.
Correlations among subsets of attributes result in different spatial shapes of clusters. Hence, the similarity between cluster objects is defined by taking into account the local correlation patterns. With this notion, the term has been introduced in simultaneously with the notion discussed above.
Different methods for correlation clustering of this type are discussed in , the relationship to different types of clustering is discussed in , see also Clustering high-dimensional data
Clustering high-dimensional data
Clustering high-dimensional data is the cluster analysis of data with anywhere from a few dozen to many thousands of dimensions. Such high-dimensional data spaces are often encountered in areas such as medicine, where DNA microarray technology can produce a large number of measurements at once, and...
.
Correlation clustering (according to this definition) can be shown to be closely related to biclustering
Biclustering
Biclustering, co-clustering, or two-mode clustering is a data mining technique which allows simultaneous clustering of the rows and columns of a matrix....
. As in biclustering, the goal is to identify groups of objects that share a correlation in some of their attributes; where the correlation is usually typical for the individual clusters.