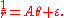Cotes' spiral
Encyclopedia
In physics
and in the mathematics
of plane curve
s, Cotes's spiral (also written Cotes' spiral and Cotes spiral) is a spiral
that is typically written in one of three forms


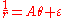
where r and θ are the radius and azimuthal angle in a polar coordinate system
, respectively, and A, k and ε are arbitrary real number
constants. These spirals are named after Roger Cotes
. The first form corresponds to an epispiral, and the second to one of Poinsot's spirals; the third form corresponds to a hyperbolic spiral
, also known as a reciprocal spiral, which is sometimes not counted as a Cotes's spiral.
The significance of Cotes's spirals for physics are in the field of classical mechanics
. These spirals are the solutions for the motion of a particle moving under a inverse-cube central force, e.g.,
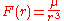
where μ is any real number
constant. A central force is one that depends only on the distance r between the moving particle and a point fixed in space, the center. In this case, the constant k of the spiral can be determined from μ and the areal velocity
of the particle h by the formula
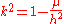
when μ < h 2 (cosine form of the spiral) and

when μ > h 2 (hyperbolic cosine form of the spiral). When μ = h 2 exactly, the particle follows the third form of the spiral
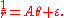
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and in the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
s, Cotes's spiral (also written Cotes' spiral and Cotes spiral) is a spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
that is typically written in one of three forms


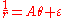
where r and θ are the radius and azimuthal angle in a polar coordinate system
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, respectively, and A, k and ε are arbitrary real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
constants. These spirals are named after Roger Cotes
Roger Cotes
Roger Cotes FRS was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as...
. The first form corresponds to an epispiral, and the second to one of Poinsot's spirals; the third form corresponds to a hyperbolic spiral
Hyperbolic spiral
thumb|200px|right|Hyperbolic spiral for a=2A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral. A hyperbolic spiral is the opposite of an Archimedean spiral and are a type of Cotes' spiral.It has the polar equation:...
, also known as a reciprocal spiral, which is sometimes not counted as a Cotes's spiral.
The significance of Cotes's spirals for physics are in the field of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. These spirals are the solutions for the motion of a particle moving under a inverse-cube central force, e.g.,
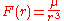
where μ is any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
constant. A central force is one that depends only on the distance r between the moving particle and a point fixed in space, the center. In this case, the constant k of the spiral can be determined from μ and the areal velocity
Areal velocity
Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
of the particle h by the formula
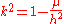
when μ < h 2 (cosine form of the spiral) and

when μ > h 2 (hyperbolic cosine form of the spiral). When μ = h 2 exactly, the particle follows the third form of the spiral