Couette flow
Encyclopedia
In fluid dynamics
, Couette flow refers to the laminar flow
of a viscous
fluid
in the space between two parallel plates, one of which is moving relative to the other. The flow is driven by virtue of viscous drag force acting on the fluid and the applied pressure gradient parallel to the plates. This type of flow is named in honor of Maurice Marie Alfred Couette, a Professor of Physics at the French university of Angers
in the late 19th century.
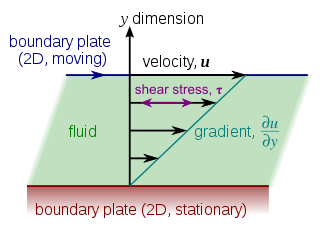
fluid motion. The simplest conceptual configuration finds two infinite, parallel plates separated by a distance h. One plate, say the top one, translates with a constant velocity u0 in its own plane. Neglecting pressure gradients, the Navier-Stokes equations
simplify to
where y is a spatial coordinate normal to the plates and u (y) is the velocity distribution. This equation reflects the assumption that the flow is uni-directional. That is, only one of the three velocity components
is non-trivial. If y originates at the lower plate, the boundary conditions are u(0) = 0 and u(h) = u0. The exact solution
can be found by integrating twice and solving for the constants using the boundary conditions.
is constant throughout the flow domain. In particular, the first derivative of the velocity, u0 / h, is constant. (This is implied by the straight-line profile in the figure.) According to Newton's Law of Viscosity
(Newtonian fluid), the shear stress is the product of this expression and the (constant) fluid viscosity
.
where
is the pressure gradient parallel to the plates and 
is fluid viscosity
. Integrating the above equation twice and applying the boundary conditions (same as in the case of Couette flow without pressure gradient) to yield the following exact solution
The shape of the above velocity profile depends on the dimensionless parameter
The pressure gradient can be positive (adverse pressure gradient) or negative (favorable pressure gradient).
It may be noted that in the limiting case of stationary plates, the flow is referred to as plane Poiseuille flow with a
symmetric (with reference to the horizontal mid-plane) parabolic velocity profile.
was interested in shear-driven flows created by rotating co-axial cylinders. He reported a mathematical result in 1923 that accounts for curvature in the flow direction having the form
where C1 and C2 are constants that depend on the rotation rates of the cylinders. (Note that r has replaced y in this result to reflect cylindrical rather than rectangular coordinates.) It is clear from this equation that curvature effects no longer allow for constant shear in the flow domain, as shown above. This model is incomplete in that it does not account for near-wall effects in finite-width cylinders, although it is a reasonable approximation if the width is large compared to the space between the cylinders. Generalizations of Taylor's basic model have also been examined. For example, the solution for the time-dependent "start-up" process can be expressed in terms of Bessel function
s.
and 
, respectively, where 
is only slightly greater than 
. In this case, curvature can be neglected locally. The physicist/mathematician Ratip Berker reported a mathematical solution for this configuration in terms of a trigonometric expansion
in the wall region. A mathematical result that accounts for both of these aspects was given only recently by Michael Wendl. His solution takes the form of an expansion of modified (hyperbolic) Bessel function
s of the first kind.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, Couette flow refers to the laminar flow
Laminar flow
Laminar flow, sometimes known as streamline flow, occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross currents...
of a viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
in the space between two parallel plates, one of which is moving relative to the other. The flow is driven by virtue of viscous drag force acting on the fluid and the applied pressure gradient parallel to the plates. This type of flow is named in honor of Maurice Marie Alfred Couette, a Professor of Physics at the French university of Angers
Angers
Angers is the main city in the Maine-et-Loire department in western France about south-west of Paris. Angers is located in the French region known by its pre-revolutionary, provincial name, Anjou, and its inhabitants are called Angevins....
in the late 19th century.
Simple conceptual configuration
Mathematical description
Couette flow is frequently used in undergraduate physics and engineering courses to illustrate shear-drivenShearing (physics)
Shearing in continuum mechanics refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material...
fluid motion. The simplest conceptual configuration finds two infinite, parallel plates separated by a distance h. One plate, say the top one, translates with a constant velocity u0 in its own plane. Neglecting pressure gradients, the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
simplify to
where y is a spatial coordinate normal to the plates and u (y) is the velocity distribution. This equation reflects the assumption that the flow is uni-directional. That is, only one of the three velocity components
is non-trivial. If y originates at the lower plate, the boundary conditions are u(0) = 0 and u(h) = u0. The exact solutioncan be found by integrating twice and solving for the constants using the boundary conditions.
Constant shear
A notable aspect of this model is that shear stressShear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
is constant throughout the flow domain. In particular, the first derivative of the velocity, u0 / h, is constant. (This is implied by the straight-line profile in the figure.) According to Newton's Law of Viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
(Newtonian fluid), the shear stress is the product of this expression and the (constant) fluid viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
.
Couette flow with pressure gradient
A more general Couette flow situation arises when a pressure gradient is imposed in a direction parallel to the plates. The Navier-Stokes equations, in this case, simplify towhere
is the pressure gradient parallel to the plates and is fluid viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. Integrating the above equation twice and applying the boundary conditions (same as in the case of Couette flow without pressure gradient) to yield the following exact solution
The shape of the above velocity profile depends on the dimensionless parameter
The pressure gradient can be positive (adverse pressure gradient) or negative (favorable pressure gradient).
It may be noted that in the limiting case of stationary plates, the flow is referred to as plane Poiseuille flow with a
symmetric (with reference to the horizontal mid-plane) parabolic velocity profile.
Taylor's idealized model
The configuration shown in the figure cannot actually be realized, as the two plates cannot extend infinitely in the flow direction. Sir Geoffrey TaylorGeoffrey Ingram Taylor
Sir Geoffrey Ingram Taylor OM was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this century".-Biography:Taylor was born in St. John's Wood, London...
was interested in shear-driven flows created by rotating co-axial cylinders. He reported a mathematical result in 1923 that accounts for curvature in the flow direction having the form
where C1 and C2 are constants that depend on the rotation rates of the cylinders. (Note that r has replaced y in this result to reflect cylindrical rather than rectangular coordinates.) It is clear from this equation that curvature effects no longer allow for constant shear in the flow domain, as shown above. This model is incomplete in that it does not account for near-wall effects in finite-width cylinders, although it is a reasonable approximation if the width is large compared to the space between the cylinders. Generalizations of Taylor's basic model have also been examined. For example, the solution for the time-dependent "start-up" process can be expressed in terms of Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s.
Finite-width model
Taylor's solution accounts for the curvature inherent in the cylindrical devices typically used to create Couette flows, but not the finite nature of the width. A complementary idealization accounts for finiteness, but not curvature. In the figure above, we might think of the "boundary plate" and the "moving plate" as the edges of two cylinders having large radii, say and , respectively, where is only slightly greater than . In this case, curvature can be neglected locally. The physicist/mathematician Ratip Berker reported a mathematical solution for this configuration in terms of a trigonometric expansionTrigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
Wendl's result for physical devices
Actual co-axial cylinder devices used to create Couette flows have both curvature and finite geometry. The latter gives rise to increased dragDrag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
in the wall region. A mathematical result that accounts for both of these aspects was given only recently by Michael Wendl. His solution takes the form of an expansion of modified (hyperbolic) Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s of the first kind.