Cover tree
Encyclopedia
The cover tree is a type of data structure
in computer science
that is specifically designed to facilitate the speed-up of a nearest neighbor search
. It is a refinement of the Navigating Net data structure, and related to a variety of other data structures developed for indexing intrinsically low-dimensional data.
The tree can be thought of as a hierarchy of levels with the top level containing the root point
and the bottom level containing every point in the metric space. Each level C is associated with an integer value i that decrements by one as the tree is descended. Each level C in the cover tree has three important properties:
s the cover tree allows for nearest neighbor searches in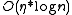
where 
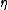is a constant associated with the dimensionality of the dataset and n is the cardinality. To compare, a basic linear search requires 
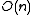, which is a much worse dependence on 
. However, in high-dimensional metric space
s the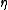
constant is non-trivial, which means it cannot be ignored in complexity analysis. Unlike other metric trees, the cover tree has a theoretical bound on its constant that is based on the dataset's expansion constant or doubling constant (in the case of approximate NN retrieval). The bound on search time is 
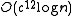where 
is the expansion constant of the dataset.
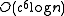time. However, this is an upper-bound, and some techniques have been implemented that seem to improve the performance in practice.
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that is specifically designed to facilitate the speed-up of a nearest neighbor search
Nearest neighbor search
Nearest neighbor search , also known as proximity search, similarity search or closest point search, is an optimization problem for finding closest points in metric spaces. The problem is: given a set S of points in a metric space M and a query point q ∈ M, find the closest point in S to q...
. It is a refinement of the Navigating Net data structure, and related to a variety of other data structures developed for indexing intrinsically low-dimensional data.
The tree can be thought of as a hierarchy of levels with the top level containing the root point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
and the bottom level containing every point in the metric space. Each level C is associated with an integer value i that decrements by one as the tree is descended. Each level C in the cover tree has three important properties:
- Nesting:
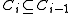
- Covering: For every point
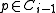, there exists a point 
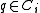such that the distance from 
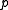to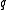 
is less than or equal to 
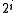and exactly one such 
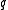is a parent of 
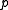. - Separation: For all points
, the distance from 
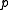to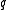 
is greater than 
.
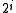Find
Like other metric treeMetric tree
A metric tree is any tree data structure specialized to index data in metric spaces. Metric trees exploit properties of metric spaces such as the triangle inequality to make accesses to the data more efficient...
s the cover tree allows for nearest neighbor searches in
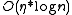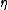where is a constant associated with the dimensionality of the dataset and n is the cardinality. To compare, a basic linear search requires 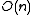, which is a much worse dependence on . However, in high-dimensional metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s the
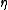constant is non-trivial, which means it cannot be ignored in complexity analysis. Unlike other metric trees, the cover tree has a theoretical bound on its constant that is based on the dataset's expansion constant or doubling constant (in the case of approximate NN retrieval). The bound on search time is 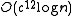where is the expansion constant of the dataset.Insert
Although cover trees provide faster searches than the naive approach, this advantage must be weighed with the additional cost of maintaining the data structure. In a naive approach adding a new point to the dataset is trivial because order does not need to be preserved, but in a cover tree it can take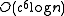 time. However, this is an upper-bound, and some techniques have been implemented that seem to improve the performance in practice.