Cramer's rule
Encyclopedia
In linear algebra
, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution. The solution is expressed in terms of the determinant
s of the (square) coefficient matrix
and of matrices obtained from it by replacing one column by the vector of right hand sides of the equations. It is named after Gabriel Cramer
(1704–1752), who published the rule in his 1750 Introduction à l'analyse des lignes courbes algébriques (Introduction to the analysis of algebraic curves), although Colin Maclaurin
also published the method in his 1748 Treatise of Algebra (and probably knew of the method as early as 1729).
where the n by n matrix
has a nonzero determinant, and the vector 
is the column vector of the variables.
Then the theorem states that in this case the system has a unique solution, whose individual values for the unknowns are given by:
where
is the matrix formed by replacing the ith column of 
by the column vector 
.
The rule holds for systems of equations with coefficients and unknowns in any field
, not just in the real number
s. It has recently been shown that Cramer's rule can be implemented in O(n3) time, which is comparable to more common methods of solving systems of linear equations, such as Gaussian elimination
.
of column vectors produces as determinant the corresponding linear combination of their determinants), and the fact that the determinant is zero whenever two columns are equal (the determinant is alternating in the columns).
Fix the index j of a column. Linearity means that if we consider only column j as variable (fixing the others arbitrarily), the resulting function (assuming matrix entries are in R) can be given by a matrix, with one row and n columns. In fact this is precisely what Laplace expansion
does, writing for certain coefficients C1,…,Cn that depend on the columns of A other than column j (the precise expression for these cofactor
s is not important here). The value det(A) is then the result of applying the one-line matrix to column j of A. If is applied to any other column k of A, then the result is the determinant of the matrix obtained from A by replacing column j by a copy of column k, which is 0 (the case of two equal columns).
Now consider a system of n linear equations in n unknowns
, whose coefficient matrix is A, with det(A) assumed to be nonzero:
If one combines these equations by taking C1 times the first equation, plus C2 times the second, and so forth until Cn times the last, then the coefficient of xj will become , while the coefficients of all other unknowns become 0; the left hand side becomes simply det(A)xj. The right hand side is , which is applied to the column vector b of the right hand sides bi. In fact what has been done here is multiply the matrix equation on the left by . Dividing by the nonzero number det(A) one finds the following equation, necessary to satisfy the system:
But by construction the numerator is determinant of the matrix obtained from A by replacing column j by b, so we get the expression of Cramers rule as necessary condition for a solution. The same procedure can be repeated for other values of j to find values for the other unknowns.
The only point that remains to prove is that these values for the unknowns, the only possible ones, to indeed together form a solution. But if the matrix A is invertible with inverse A−1, then will be a solution, thus showing its existence. To see that A is invertible when det(A) is nonzero, consider the n by n matrix M obtained by stacking the one-line matrices on top of each other for j = 1, 2, …, n (this gives the adjugate matrix
for A). It was shown that where appears at the position j; from this it follows that . Therefore
completing the proof.
where Adj(A) denotes the adjugate matrix
of A, det(A) is the determinant, and I is the identity matrix
. If det(A) is invertible in R, then the inverse matrix of A is
If R is a field
(such as the field of real numbers), then this gives a formula for the inverse of A, provided det(A) ≠ 0. In fact, this formula will work whenever R is a commutative ring
, provided that det(A) is a unit
. If det(A) is not a unit, then A is not invertible.
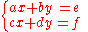which in matrix format is 
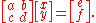Then, x and y can be found with Cramer's rule as
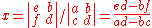and
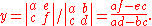
The rules for 3×3 are similar. Given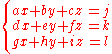
which in matrix format is
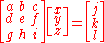the values of x, y and z can be found as follows:
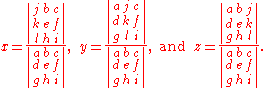
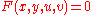and 
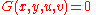. When u and v are independent variables, we can define 
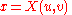and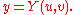 
Finding an equation for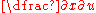
is a trivial application of Cramer's rule.
First, calculate the first derivatives of F, G, x, and y: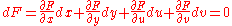
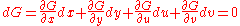
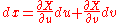
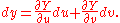
Substituting dx, dy into dF and dG, we have:
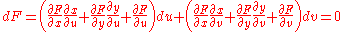
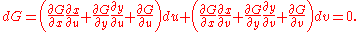
Since u, v are both independent, the coefficients of du, dv must be zero. So we can write out equations for the coefficients: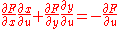
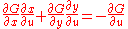
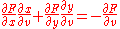
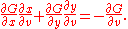
Now, by Cramer's rule, we see that:
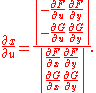
This is now a formula in terms of two Jacobians: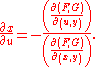
Similar formulae can be derived for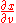
, 
, 
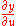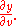
problem whose constraint matrix is totally unimodular and whose right-hand side is integer, has integer basic solutions. This makes the integer program substantially easier to solve.
Given the system of equations
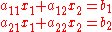
it can be considered as an equation between vectors
The area of the parallelogram determined by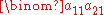
and 
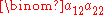is given by the determinant of the system of equations:
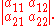
In general, when there are more variables and equations, the determinant of
vectors of length 
will give the volume of the parallelepiped
determined by those vectors in the
-th dimensional Euclidean space
.
Therefore the area of the parallelogram determined by
and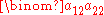 
has to be 
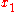times the area of the first one since one of the sides has been multiplied by this factor.
Now, this last parallelogram, by Cavalieri's principle
, has the same area as the parallelogram determined by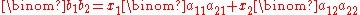
and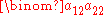 
.
Equating the areas of this last and the second parallelogram gives the equation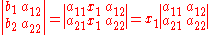
from which Cramer's rule follows.
Cramer's rule applies to the case where the coefficient determinant is nonzero. In the contrary case the system is either incompatible or indeterminate, based on the values of the determinants only for 2x2 systems.
For 3x3 or higher systems, the only thing one can say when the coefficient determinant equals zero is: if any of the "numerator" determinants are nonzero, then the system must be incompatible. However, the converse is false: having all determinants zero does not imply that the system is indeterminate. A simple example where all determinants vanish but the system is still incompatible is the 3x3 system x+y+z=1, x+y+z=2, x+y+z=3.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution. The solution is expressed in terms of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s of the (square) coefficient matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and of matrices obtained from it by replacing one column by the vector of right hand sides of the equations. It is named after Gabriel Cramer
Gabriel Cramer
Gabriel Cramer was a Swiss mathematician, born in Geneva. He showed promise in mathematics from an early age. At 18 he received his doctorate and at 20 he was co-chair of mathematics.In 1728 he proposed a solution to the St...
(1704–1752), who published the rule in his 1750 Introduction à l'analyse des lignes courbes algébriques (Introduction to the analysis of algebraic curves), although Colin Maclaurin
Colin Maclaurin
Colin Maclaurin was a Scottish mathematician who made important contributions to geometry and algebra. The Maclaurin series, a special case of the Taylor series, are named after him....
also published the method in his 1748 Treatise of Algebra (and probably knew of the method as early as 1729).
General case
Consider a system of n linear equations for n unknowns, represented in matrix multiplication form as follows: |
 |
where the n by n matrix
has a nonzero determinant, and the vector is the column vector of the variables.Then the theorem states that in this case the system has a unique solution, whose individual values for the unknowns are given by:
where
is the matrix formed by replacing the ith column of by the column vector .The rule holds for systems of equations with coefficients and unknowns in any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, not just in the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. It has recently been shown that Cramer's rule can be implemented in O(n3) time, which is comparable to more common methods of solving systems of linear equations, such as Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
.
Proof
The proof for Cramer's rule is very simple; in fact, it uses just two properties of determinants: linearity with respect to any given column (taking for that column a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of column vectors produces as determinant the corresponding linear combination of their determinants), and the fact that the determinant is zero whenever two columns are equal (the determinant is alternating in the columns).
Fix the index j of a column. Linearity means that if we consider only column j as variable (fixing the others arbitrarily), the resulting function (assuming matrix entries are in R) can be given by a matrix, with one row and n columns. In fact this is precisely what Laplace expansion
Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
does, writing for certain coefficients C1,…,Cn that depend on the columns of A other than column j (the precise expression for these cofactor
Cofactor (linear algebra)
In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
s is not important here). The value det(A) is then the result of applying the one-line matrix to column j of A. If is applied to any other column k of A, then the result is the determinant of the matrix obtained from A by replacing column j by a copy of column k, which is 0 (the case of two equal columns).
Now consider a system of n linear equations in n unknowns
, whose coefficient matrix is A, with det(A) assumed to be nonzero:If one combines these equations by taking C1 times the first equation, plus C2 times the second, and so forth until Cn times the last, then the coefficient of xj will become , while the coefficients of all other unknowns become 0; the left hand side becomes simply det(A)xj. The right hand side is , which is applied to the column vector b of the right hand sides bi. In fact what has been done here is multiply the matrix equation on the left by . Dividing by the nonzero number det(A) one finds the following equation, necessary to satisfy the system:
But by construction the numerator is determinant of the matrix obtained from A by replacing column j by b, so we get the expression of Cramers rule as necessary condition for a solution. The same procedure can be repeated for other values of j to find values for the other unknowns.
The only point that remains to prove is that these values for the unknowns, the only possible ones, to indeed together form a solution. But if the matrix A is invertible with inverse A−1, then will be a solution, thus showing its existence. To see that A is invertible when det(A) is nonzero, consider the n by n matrix M obtained by stacking the one-line matrices on top of each other for j = 1, 2, …, n (this gives the adjugate matrix
Adjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
for A). It was shown that where appears at the position j; from this it follows that . Therefore
completing the proof.
Finding inverse matrix
Let A be an n×n matrix. Thenwhere Adj(A) denotes the adjugate matrix
Adjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
of A, det(A) is the determinant, and I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. If det(A) is invertible in R, then the inverse matrix of A is
If R is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(such as the field of real numbers), then this gives a formula for the inverse of A, provided det(A) ≠ 0. In fact, this formula will work whenever R is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, provided that det(A) is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
. If det(A) is not a unit, then A is not invertible.
Explicit formulas for small systems
Consider the linear system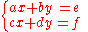 which in matrix format is 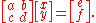Then, x and y can be found with Cramer's rule as 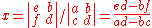and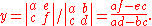The rules for 3×3 are similar. Given
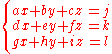which in matrix format is 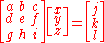the values of x, y and z can be found as follows: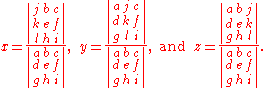Differential geometry
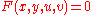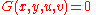Cramer's rule is also extremely useful for solving problems in differential geometry. Consider the two equations and . When u and v are independent variables, we can define 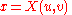and 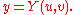Finding an equation for
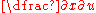is a trivial application of Cramer's rule.First, calculate the first derivatives of F, G, x, and y:
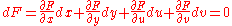
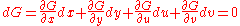
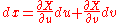
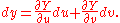
Substituting dx, dy into dF and dG, we have:
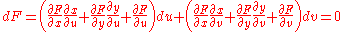
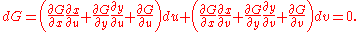
Since u, v are both independent, the coefficients of du, dv must be zero. So we can write out equations for the coefficients:
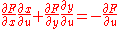
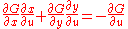
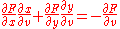
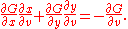
Now, by Cramer's rule, we see that:
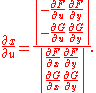
This is now a formula in terms of two Jacobians:
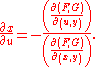
Similar formulae can be derived for
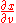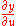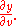
, , Integer programming
Cramer's rule can be used to prove that an integer programmingInteger programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming, which is also known as mixed integer programming.Integer programming is NP-hard...
problem whose constraint matrix is totally unimodular and whose right-hand side is integer, has integer basic solutions. This makes the integer program substantially easier to solve.
Ordinary differential equations
Cramer's rule is used to derive the general solution to an inhomogeneous linear differential equation by the method of variation of parameters.Geometric interpretation
Cramer's rule has a geometric interpretation that can be considered also a proof or simply giving insight about its geometric nature. These geometric arguments work in general and not only in the case of two equations with two unknowns presented here.Given the system of equations
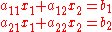
it can be considered as an equation between vectors
The area of the parallelogram determined by
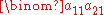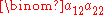and is given by the determinant of the system of equations: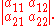In general, when there are more variables and equations, the determinant of
vectors of length will give the volume of the parallelepipedParallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
determined by those vectors in the
-th dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Therefore the area of the parallelogram determined by
and 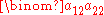has to be 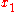times the area of the first one since one of the sides has been multiplied by this factor.Now, this last parallelogram, by Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
, has the same area as the parallelogram determined by
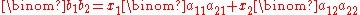and 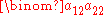.Equating the areas of this last and the second parallelogram gives the equation
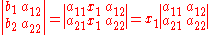
from which Cramer's rule follows.
Incompatible and indeterminate cases
A system of equations is said to be incompatible when there are no solutions and it is called indeterminate when there is more than one solution. For linear equations, an indeterminate system will have infinitely many solutions (if it is over an infinite field), since the solutions can be expressed in terms of one or more parameters that can take arbitrary values.Cramer's rule applies to the case where the coefficient determinant is nonzero. In the contrary case the system is either incompatible or indeterminate, based on the values of the determinants only for 2x2 systems.
For 3x3 or higher systems, the only thing one can say when the coefficient determinant equals zero is: if any of the "numerator" determinants are nonzero, then the system must be incompatible. However, the converse is false: having all determinants zero does not imply that the system is indeterminate. A simple example where all determinants vanish but the system is still incompatible is the 3x3 system x+y+z=1, x+y+z=2, x+y+z=3.