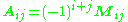Cofactor (linear algebra)
Encyclopedia
In linear algebra
, the cofactor (sometimes called adjunct, see below) describes a particular construction that is useful for calculating both the determinant
and inverse of square matrices
. Specifically the cofactor of the (i, j) entry of a matrix, also known as the (i, j) cofactor of that matrix, is the sign
ed minor
of that entry.
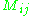is termed the minor for entry 
.
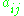If i + j is an even number, the cofactor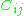
of 
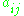coincides with its minor: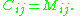
Otherwise, it is equal to the additive inverse of its minor: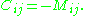
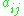, also known as the i,j, or (i,j), or (i,j)th minor of A, is denoted by 
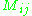and is defined to be the determinant of the submatrix obtained by removing from A its i-th row and j-th column.
It follows: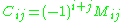
and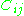
called the cofactor of 
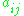, also referred to as the i,j, (i,j) or (i,j)th cofactor of A.
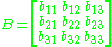
suppose we wish to find the cofactor C23. The minor M23 is the determinant of the above matrix with row 2 and column 3 removed.
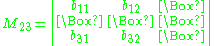yields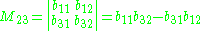 
Using the given definition it follows that
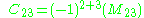
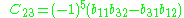
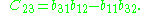
Note: the vertical lines are an equivalent notation for det(matrix)
matrix
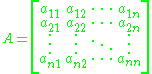
The determinant of A (denoted det(A)) can be written as the sum of the cofactors of any row or column of the matrix multiplied by the entries that generated them.
Cofactor expansion along the jth column:
Cofactor expansion along the ith row:
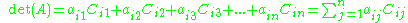
matrix A is the matrix whose (i,j) entry is the cofactor Cij of A. For instance, if A is
the cofactor matrix of A is
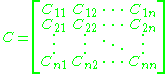
where Cij is the cofactor of aij.
of the matrix of cofactors and is very useful due to its relation to the inverse of A.
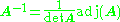
The matrix of cofactors
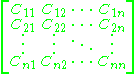
when transposed becomes
Using this notation the inverse matrix is written this way: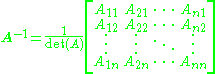
Keep in mind that adjunct is not adjugate or adjoint
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the cofactor (sometimes called adjunct, see below) describes a particular construction that is useful for calculating both the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and inverse of square matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Specifically the cofactor of the (i, j) entry of a matrix, also known as the (i, j) cofactor of that matrix, is the sign
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
ed minor
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
of that entry.
Informal approach to minors and cofactors
Finding the minors of a matrix A is a multi-step process:- Choose an entry
from the matrix. - Cross out the entries that lie in the corresponding row
and column 
. - Rewrite the matrix without the marked entries.
- Obtain the determinant
of this new matrix.
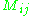is termed the minor for entry 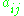.If i + j is an even number, the cofactor
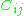of 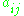coincides with its minor: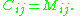Otherwise, it is equal to the additive inverse of its minor:
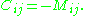
Formal definition
If A is a square matrix, then the minor of its entry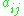, also known as the i,j, or (i,j), or (i,j)th minor of A, is denoted by 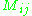and is defined to be the determinant of the submatrix obtained by removing from A its i-th row and j-th column.It follows:
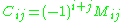
and
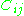called the cofactor of 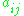, also referred to as the i,j, (i,j) or (i,j)th cofactor of A.Example
Given the matrix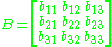suppose we wish to find the cofactor C23. The minor M23 is the determinant of the above matrix with row 2 and column 3 removed.
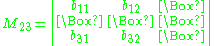yields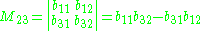 Using the given definition it follows that
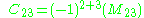
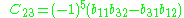
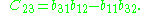
Note: the vertical lines are an equivalent notation for det(matrix)
Cofactor expansion
Given the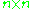 matrix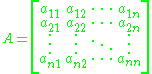The determinant of A (denoted det(A)) can be written as the sum of the cofactors of any row or column of the matrix multiplied by the entries that generated them.
Cofactor expansion along the jth column:
Cofactor expansion along the ith row:
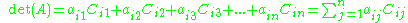
Matrix of cofactors
The matrix of cofactors for an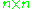 matrix A is the matrix whose (i,j) entry is the cofactor Cij of A. For instance, if A isthe cofactor matrix of A is
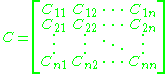
where Cij is the cofactor of aij.
Adjugate
The adjugate matrix is the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the matrix of cofactors and is very useful due to its relation to the inverse of A.
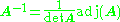
The matrix of cofactors
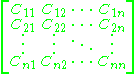
when transposed becomes
A remark about different notations
In some books, including the so called "bible of matrix theory" instead of cofactor the term adjunct is used. Moreover, it is denoted as Aij and defined in the same way as cofactor:
Using this notation the inverse matrix is written this way:
Keep in mind that adjunct is not adjugate or adjoint
Adjoint
In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
.
See also
- Linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
- Matrix (mathematics)Matrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
- Minor (linear algebra)Minor (linear algebra)In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
- Adjugate matrixAdjugate matrixIn linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
External links
- MIT Linear Algebra Lecture on Cofactors at Google Video, from MIT OpenCourseWare
- PlanetMath