
Critical pair (logic)
Encyclopedia
In mathematical logic
, a critical pair arises in term rewriting systems where rewrite rules overlap to yield two different terms.
For example, in the term rewriting system with rules
the only critical pair is then (g(x,z), f(x,z)).
When one side of the critical pair reduces
to the other, we say that the critical pair is convergent. Where one side of the critical pair is identical to the other, we say that the critical pair is trivial.
Note that if the term rewriting system is not confluent
, the critical pair may not converge, so critical pairs are potential sources where confluence will fail. In fact, we have the critical pair lemma, which states that a term rewriting system is weakly confluent if all critical pairs are convergent. Thus, to find out if a term rewriting system is weakly confluent, it suffices to test all critical pairs and see if they are convergent. This makes it possible to find out algorithmically if a term rewriting system is weakly confluent or not.
Weak confluence clearly implies convergent critical pairs: if any critical pair (a, b) arises, then a and b have common reduct
and thus the critical pair is convergent.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a critical pair arises in term rewriting systems where rewrite rules overlap to yield two different terms.
For example, in the term rewriting system with rules
-
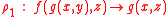
-
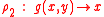 ,
,
the only critical pair is then (g(x,z), f(x,z)).
When one side of the critical pair reduces
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
to the other, we say that the critical pair is convergent. Where one side of the critical pair is identical to the other, we say that the critical pair is trivial.
Note that if the term rewriting system is not confluent
Confluence (term rewriting)
In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...
, the critical pair may not converge, so critical pairs are potential sources where confluence will fail. In fact, we have the critical pair lemma, which states that a term rewriting system is weakly confluent if all critical pairs are convergent. Thus, to find out if a term rewriting system is weakly confluent, it suffices to test all critical pairs and see if they are convergent. This makes it possible to find out algorithmically if a term rewriting system is weakly confluent or not.
Weak confluence clearly implies convergent critical pairs: if any critical pair (a, b) arises, then a and b have common reduct
Reduct
In universal algebra and in model theory, a reduct of an algebraic structure is obtained by omitting some of the operations and relations of that structure...
and thus the critical pair is convergent.

