
Crofton formula
Encyclopedia
In mathematics
, the Crofton formula, named after Morgan Crofton
(1826–1915), is a classic result of integral geometry
relating the length of a curve to the expected
number of times a "random" line
intersects it.
. Given an oriented line l, let nγ(l) be the number of points at which γ and l intersect. We can parametrize the general line l by the direction φ in which it points and its signed distance p from the origin
. The Crofton formula expresses the arc length of the curve γ in terms of an integral
over the space of all oriented lines:
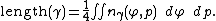
The differential form

is invariant under rigid motions
, so it is a natural integration measure for speaking of an "average" number of intersections.
over concatenation of curves, so it suffices to prove the formula for a single line segment. Since the right-hand side does not depend on the positioning of the line segment, it must equal some function of the segment's length, and by additivity the function must be linear. It remains only to determine the factor of 1/4; this is easily done by computing both sides when γ is the unit circle
.
of the space of unoriented lines. The Crofton formula is often stated in terms of the corresponding density in the latter space, in which the numerical factor is not 1/4 but 1/2. Since a convex curve intersects almost every
line either twice or not at all, the unoriented Crofton formula for convex curves can be stated without numerical factors: the measure of the set of straight lines which intersect a convex curve is equal to its length.
The Crofton formula generalizes to any Riemannian
surface; the integral is then performed with the natural measure on the space of geodesic
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Crofton formula, named after Morgan Crofton
Morgan Crofton
Morgan Crofton was a mathematician who contributed to the field of geometric probability theory. He also worked with James Joseph Sylvester and contributed an article on probability to the 9th edition of the Encyclopædia Britannica...
(1826–1915), is a classic result of integral geometry
Integral geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...
relating the length of a curve to the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
number of times a "random" line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
intersects it.
Statement
Suppose γ is a rectifiable plane curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
. Given an oriented line l, let nγ(l) be the number of points at which γ and l intersect. We can parametrize the general line l by the direction φ in which it points and its signed distance p from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
. The Crofton formula expresses the arc length of the curve γ in terms of an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over the space of all oriented lines:
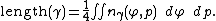
The differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...

is invariant under rigid motions
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, so it is a natural integration measure for speaking of an "average" number of intersections.
Proof sketch
Both sides of the Crofton formula are additiveAdditive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
over concatenation of curves, so it suffices to prove the formula for a single line segment. Since the right-hand side does not depend on the positioning of the line segment, it must equal some function of the segment's length, and by additivity the function must be linear. It remains only to determine the factor of 1/4; this is easily done by computing both sides when γ is the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.
Other forms
The space of oriented lines is a double coverCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of the space of unoriented lines. The Crofton formula is often stated in terms of the corresponding density in the latter space, in which the numerical factor is not 1/4 but 1/2. Since a convex curve intersects almost every
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
line either twice or not at all, the unoriented Crofton formula for convex curves can be stated without numerical factors: the measure of the set of straight lines which intersect a convex curve is equal to its length.
The Crofton formula generalizes to any Riemannian
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
surface; the integral is then performed with the natural measure on the space of geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s.
Applications
Crofton's formula yields elegant proofs of the following results, among others:- Between two nested, convex, closed curves, the inner one is shorter.
- Barbier's theoremBarbier's theoremBarbier's theorem, a basic result on curves of constant width first proved by Joseph Emile Barbier, states that the perimeter of any curve of constant width w is πw....
: a curve of constant widthCurve of constant widthIn geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.More generally, any compact...
w has a perimeter of πw. - The isoperimetric inequality: among closed curves with a given perimeter, the circle gives the unique maximum area.
See also
- Buffon's noodleBuffon's noodleIn geometric probability, the problem of Buffon's noodle is a variation on the well-known problem of Buffon's needle, named after Georges-Louis Leclerc, Comte de Buffon who lived in the 18th century...
- The Radon transformRadon transformthumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
can be viewed as a measure-theoretic generalization of the Cauchy–Crofton formula.
External links
- Cauchy–Crofton formula page, with demonstration applets

