Cuban prime
Encyclopedia
A cuban prime is a prime number
that is a solution to one of two different specific equations involving third powers of x and y. The first of these equations is:
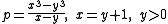
and the first few cuban primes from this equation are :
7, 19
, 37
, 61
, 127
, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669, 16651, 19441, 19927, 22447, 23497, 24571, 25117, 26227
The general cuban prime of this kind can be rewritten as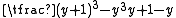
, which simplifies to 
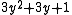. This is exactly the general form of a centered hexagonal number
; that is, all of these cuban primes are centered hexagonal.
This kind of cuban primes has been researched by A. J. C. Cunningham, in a paper entitled On quasi-Mersennian numbers.
the largest known has 65537 digits with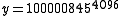
http://primes.utm.edu/primes/page.php?id=76705#comments, found by Jens Kruse Andersen.
The second of these equations is:
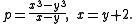
It simplifies to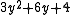
. The first few cuban primes on this form are :
This kind of cuban primes have also been researched by Cunningham, in his book Binomial Factorisations.
The name "cuban prime" has to do with the role cubes
(third powers) play in the equations, and has nothing to do with Cuba
.
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
that is a solution to one of two different specific equations involving third powers of x and y. The first of these equations is:
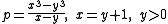
and the first few cuban primes from this equation are :
7, 19
19 (number)
19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 37
37 (number)
37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
, 61
61 (number)
61 is the natural number following 60 and preceding 62.-In mathematics:It is the 18th prime number. The previous is 59, with which it comprises a twin prime. Sixty-one is a cuban prime of the form p = / , x = y + 1....
, 127
127 (number)
127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime...
, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669, 16651, 19441, 19927, 22447, 23497, 24571, 25117, 26227
The general cuban prime of this kind can be rewritten as
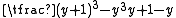, which simplifies to 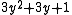. This is exactly the general form of a centered hexagonal numberCentered hexagonal number
A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice....
; that is, all of these cuban primes are centered hexagonal.
This kind of cuban primes has been researched by A. J. C. Cunningham, in a paper entitled On quasi-Mersennian numbers.
the largest known has 65537 digits with
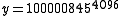http://primes.utm.edu/primes/page.php?id=76705#comments, found by Jens Kruse Andersen.The second of these equations is:
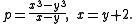
It simplifies to
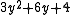. The first few cuban primes on this form are :- 13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313
This kind of cuban primes have also been researched by Cunningham, in his book Binomial Factorisations.
The name "cuban prime" has to do with the role cubes
Cube (arithmetic)
In arithmetic and algebra, the cube of a number n is its third power — the result of the number multiplying by itself three times:...
(third powers) play in the equations, and has nothing to do with Cuba
Cuba
The Republic of Cuba is an island nation in the Caribbean. The nation of Cuba consists of the main island of Cuba, the Isla de la Juventud, and several archipelagos. Havana is the largest city in Cuba and the country's capital. Santiago de Cuba is the second largest city...
.