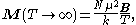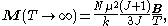Curie's law
Encyclopedia
In a paramagnetic material the magnetization
of the material is (approximately) directly proportional to an applied magnetic field
. However, if the material is heated, this proportionality is reduced: for a fixed value of the field, the magnetization is (approximately) inversely proportional to temperature
. This fact is encapsulated by Curie's law:
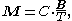
where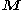 is the resulting magnetisation
is the resulting magnetisation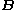 is the magnetic field, measured in teslas
is the magnetic field, measured in teslas
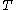 is absolute temperature, measured in kelvin
is absolute temperature, measured in kelvin
s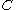 is a material-specific Curie constant.
is a material-specific Curie constant.
This relation was discovered experimentally (by fitting the results to a correctly guessed model) by Pierre Curie
. It only holds for high temperatures, or weak magnetic fields. As the derivations below
show, the magnetization saturates in the opposite limit of low temperatures, or strong fields.
of a paramagnet concentrates on the particles which compose it which do not interact with each other. Each particle has a magnetic moment
given by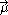 . The energy
. The energy
of a magnetic moment
in a magnetic field is given by
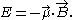
, we are going to work with a 2-state particle: it may either align its magnetic moment with the magnetic field, or against it. So the only possible values of magnetic moment are then and
and 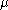 . If so, then such a particle has only two possible energies
. If so, then such a particle has only two possible energies
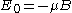
and
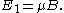
When one seeks the magnetization of a paramagnet, one is interested in the likelihood of a particle to align itself with the field. In other words, one seeks the expectation value of the magnetization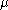 :
: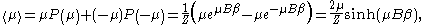
where the probability
of a configuration is given by its Boltzmann factor
, and
the partition function
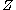 provides the necessary normalization
provides the necessary normalization
for probabilities (so that the sum
of all of them is unity.)
The partition function of one particle is:
Therefore, in this simple case we have: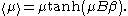
This is magnetization of one particle, the total magnetization of the solid
is given by
The formula
above is known as the Langevin paramagnetic equation.
Pierre Curie
found an approximation to this law
which applies to the relatively high temperatures and low magnetic fields used in his experiments. Let's see what happens to the magnetization as we specialize it to large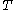 and small
and small 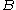 . As temperature increases and magnetic field decreases, the argument of hyperbolic tangent decreases. Another way to say this is
. As temperature increases and magnetic field decreases, the argument of hyperbolic tangent decreases. Another way to say this is
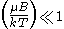
this is sometimes called the Curie regime. We also know that if , then
, then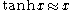
so
with a Curie constant given by . Also, in the opposite regime
. Also, in the opposite regime
of low temperatures or high fields, tends to a maximum value of
tends to a maximum value of 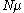 ,
,
corresponding to all the particles being completely aligned with the field.
At low magnetic fields or high temperature, however, a simple Curie law is again obtained (where is the total angular momentum quantum number):
is the total angular momentum quantum number):
in spherical coordinates, and the energy for one of them will be:
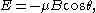
where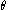 is the angle between the magnetic moment and
is the angle between the magnetic moment and
the magnetic field (which we take to be pointing in the
coordinate.) The corresponding partition function is

We see there is no dependence on the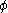 angle, and also we can
angle, and also we can
change variables to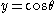 to obtain
to obtain

Now, the expected value of the component of the magnetization (the other two are seen to be null (due to integration over
component of the magnetization (the other two are seen to be null (due to integration over  ), as they should) will be given by
), as they should) will be given by
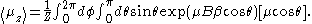
To simplify the calculation, we see this can be written as a differentiation of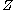 :
:
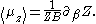
(This approach can also be used for the model above, but the calculation was so simple this
is not so helpful.)
Carrying out the derivation we find
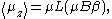
where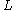 is the Langevin function:
is the Langevin function:
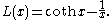
This function would appear to be singular for small , but it is not,
, but it is not,
since the two singular terms cancel each other. In fact, its behavior for small arguments is
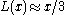 , so the Curie limit also applies, but with a Curie constant
, so the Curie limit also applies, but with a Curie constant
three times smaller in this case. Similarly, the function saturates at for large values of its argument, and the opposite limit is likewise recovered.
for large values of its argument, and the opposite limit is likewise recovered.
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
of the material is (approximately) directly proportional to an applied magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. However, if the material is heated, this proportionality is reduced: for a fixed value of the field, the magnetization is (approximately) inversely proportional to temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. This fact is encapsulated by Curie's law:
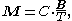
where
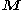 is the resulting magnetisation
is the resulting magnetisation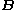 is the magnetic field, measured in teslas
is the magnetic field, measured in teslasTesla (unit)
The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
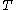 is absolute temperature, measured in kelvin
is absolute temperature, measured in kelvinKelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s
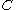 is a material-specific Curie constant.
is a material-specific Curie constant.This relation was discovered experimentally (by fitting the results to a correctly guessed model) by Pierre Curie
Pierre Curie
Pierre Curie was a French physicist, a pioneer in crystallography, magnetism, piezoelectricity and radioactivity, and Nobel laureate. He was the son of Dr. Eugène Curie and Sophie-Claire Depouilly Curie ...
. It only holds for high temperatures, or weak magnetic fields. As the derivations below
show, the magnetization saturates in the opposite limit of low temperatures, or strong fields.
Derivation with quantum statistical mechanics
A simple modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of a paramagnet concentrates on the particles which compose it which do not interact with each other. Each particle has a magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
given by
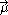 . The energy
. The energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of a magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
in a magnetic field is given by
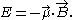
Two-state (spin-1/2) particles
To simplify the calculationCalculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
, we are going to work with a 2-state particle: it may either align its magnetic moment with the magnetic field, or against it. So the only possible values of magnetic moment are then
 and
and 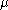 . If so, then such a particle has only two possible energies
. If so, then such a particle has only two possible energies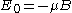
and
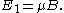
When one seeks the magnetization of a paramagnet, one is interested in the likelihood of a particle to align itself with the field. In other words, one seeks the expectation value of the magnetization
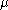 :
: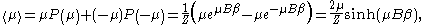
where the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of a configuration is given by its Boltzmann factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
, and
the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
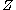 provides the necessary normalization
provides the necessary normalizationNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
for probabilities (so that the sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of all of them is unity.)
The partition function of one particle is:

Therefore, in this simple case we have:
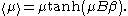
This is magnetization of one particle, the total magnetization of the solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
is given by
The formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
above is known as the Langevin paramagnetic equation.
Pierre Curie
Pierre Curie
Pierre Curie was a French physicist, a pioneer in crystallography, magnetism, piezoelectricity and radioactivity, and Nobel laureate. He was the son of Dr. Eugène Curie and Sophie-Claire Depouilly Curie ...
found an approximation to this law
Law
Law is a system of rules and guidelines which are enforced through social institutions to govern behavior, wherever possible. It shapes politics, economics and society in numerous ways and serves as a social mediator of relations between people. Contract law regulates everything from buying a bus...
which applies to the relatively high temperatures and low magnetic fields used in his experiments. Let's see what happens to the magnetization as we specialize it to large
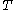 and small
and small 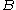 . As temperature increases and magnetic field decreases, the argument of hyperbolic tangent decreases. Another way to say this is
. As temperature increases and magnetic field decreases, the argument of hyperbolic tangent decreases. Another way to say this is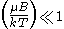
this is sometimes called the Curie regime. We also know that if
 , then
, then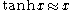
so
with a Curie constant given by
 . Also, in the opposite regime
. Also, in the opposite regimeof low temperatures or high fields,
 tends to a maximum value of
tends to a maximum value of 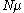 ,
,corresponding to all the particles being completely aligned with the field.
General case
When the particles have an arbitrary spin (any number of spin states), the formula is a bit more complicated. For this more general formula and its derivation, see the article: Brillouin function. As the spin approaches infinity, the formula for the magnetization approaches the classical value derived in the following section.At low magnetic fields or high temperature, however, a simple Curie law is again obtained (where
 is the total angular momentum quantum number):
is the total angular momentum quantum number):Derivation with classical statistical mechanics
An alternative treatment applies when the paramagnetons are imagined to be classical, freely-rotating magnetic moments. In this case, their position will be determined by their anglesAngles
The Angles is a modern English term for a Germanic people who took their name from the ancestral cultural region of Angeln, a district located in Schleswig-Holstein, Germany...
in spherical coordinates, and the energy for one of them will be:
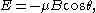
where
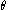 is the angle between the magnetic moment and
is the angle between the magnetic moment andthe magnetic field (which we take to be pointing in the

coordinate.) The corresponding partition function is

We see there is no dependence on the
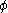 angle, and also we can
angle, and also we canchange variables to
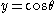 to obtain
to obtain
Now, the expected value of the
 component of the magnetization (the other two are seen to be null (due to integration over
component of the magnetization (the other two are seen to be null (due to integration over  ), as they should) will be given by
), as they should) will be given by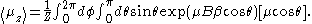
To simplify the calculation, we see this can be written as a differentiation of
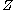 :
: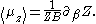
(This approach can also be used for the model above, but the calculation was so simple this
is not so helpful.)
Carrying out the derivation we find
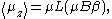
where
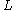 is the Langevin function:
is the Langevin function: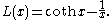
This function would appear to be singular for small
 , but it is not,
, but it is not,since the two singular terms cancel each other. In fact, its behavior for small arguments is
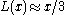 , so the Curie limit also applies, but with a Curie constant
, so the Curie limit also applies, but with a Curie constantthree times smaller in this case. Similarly, the function saturates at
 for large values of its argument, and the opposite limit is likewise recovered.
for large values of its argument, and the opposite limit is likewise recovered.