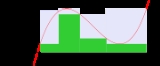
Darboux integral
Encyclopedia
In real analysis
, a branch of mathematics
, the Darboux integral or Darboux sum is one possible definition of the integral
of a function. Darboux integrals are equivalent to Riemann integral
s, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal. Darboux integrals have the advantage of being simpler to define than Riemann integrals. Darboux integrals are named after their discoverer, Gaston Darboux.
[a,b] is a finite sequence of values xi such that

Each interval [xi−1,xi] is called a subinterval of the partition. Let ƒ:[a,b]→R be a bounded function, and let
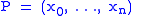
be a partition of [a,b]. Let
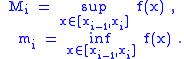
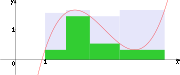 The upper Darboux sum of ƒ with respect to P is
The upper Darboux sum of ƒ with respect to P is

The lower Darboux sum of ƒ with respect to P is

The upper Darboux integral of ƒ is
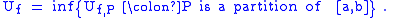
The lower Darboux integral of ƒ is
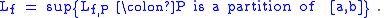
If Uƒ = Lƒ, then we say that ƒ is Darboux-integrable and set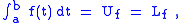
the common value of the upper and lower Darboux integrals.
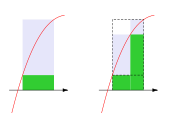 A refinement of the partition
A refinement of the partition

is a partition
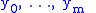
such that for every i with
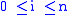
there is an integer r(i) such that
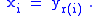
In other words, to make a refinement, cut the subintervals into smaller pieces and do not remove any existing cuts. If
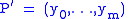
is a refinement of

then
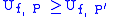
and
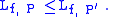
If P1, P2 are two partitions of the same interval (one need not be a refinement of the other), then
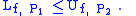 .
.
It follows that

Riemann sums always lie between the corresponding lower and upper Darboux sums. Formally, if

and
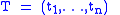
together make a tagged partition

(as in the definition of the Riemann integral
), and if the Riemann sum of ƒ corresponding to P and T is R, then
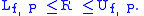
From the previous fact, Riemann integrals are at least as strong as Darboux integrals: If the Darboux integral exists, then the upper and lower Darboux sums corresponding to a sufficiently fine partition will be close to the value of the integral, so any Riemann sum over the same partition will also be close to the value of the integral. It is not hard to see that there is a tagged partition that comes arbitrarily close to the value of the upper Darboux integral or lower Darboux integral, and consequently, if the Riemann integral exists, then the Darboux integral must exist as well.
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Darboux integral or Darboux sum is one possible definition of the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function. Darboux integrals are equivalent to Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
s, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of the two integrals, if they exist, are equal. Darboux integrals have the advantage of being simpler to define than Riemann integrals. Darboux integrals are named after their discoverer, Gaston Darboux.
Definition
A partition of an intervalPartition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
[a,b] is a finite sequence of values xi such that

Each interval [xi−1,xi] is called a subinterval of the partition. Let ƒ:[a,b]→R be a bounded function, and let
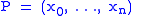
be a partition of [a,b]. Let
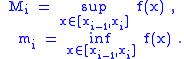


The lower Darboux sum of ƒ with respect to P is

The upper Darboux integral of ƒ is
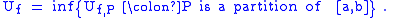
The lower Darboux integral of ƒ is
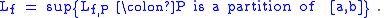
If Uƒ = Lƒ, then we say that ƒ is Darboux-integrable and set
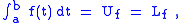
the common value of the upper and lower Darboux integrals.
Facts about the Darboux integral


is a partition
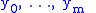
such that for every i with
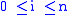
there is an integer r(i) such that
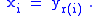
In other words, to make a refinement, cut the subintervals into smaller pieces and do not remove any existing cuts. If
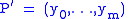
is a refinement of

then
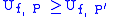
and
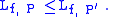
If P1, P2 are two partitions of the same interval (one need not be a refinement of the other), then
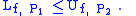 .
.It follows that

Riemann sums always lie between the corresponding lower and upper Darboux sums. Formally, if

and
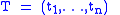
together make a tagged partition

(as in the definition of the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
), and if the Riemann sum of ƒ corresponding to P and T is R, then
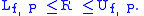
From the previous fact, Riemann integrals are at least as strong as Darboux integrals: If the Darboux integral exists, then the upper and lower Darboux sums corresponding to a sufficiently fine partition will be close to the value of the integral, so any Riemann sum over the same partition will also be close to the value of the integral. It is not hard to see that there is a tagged partition that comes arbitrarily close to the value of the upper Darboux integral or lower Darboux integral, and consequently, if the Riemann integral exists, then the Darboux integral must exist as well.
See also
- Regulated integralRegulated integralIn mathematics, the regulated integral is a definition of integration for regulated functions, which are defined to be uniform limits of step functions. The use of the regulated integral instead of the Riemann integral has been advocated by Nicolas Bourbaki and Jean Dieudonné.-Definition on step...
- Lebesgue integrationLebesgue integrationIn mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...

