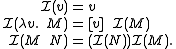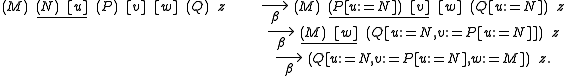De Bruijn notation
Encyclopedia
In mathematical logic
, the De Bruijn notation is a syntax for terms in the λ calculus invented by the Dutch
mathematician
Nicolaas Govert de Bruijn
. It can be seen as a reversal of the usual syntax for the λ calculus where the argument in an application is placed next to its corresponding binder in the function
instead of after the latter's body.
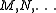) in the De Bruijn notation are either variables (
), or have one of two wagon prefixes. The abstractor wagon, written 
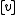, corresponds to the usual λ-binder of the λ calculus, and the applicator wagon, written 
, corresponds to the argument in an application in the λ calculus.
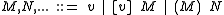
Terms in the traditional syntax can be converted to the De Bruijn notation by defining an inductive function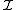
for which:
All operations on λ-terms commute with respect to the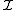
translation. For example, the usual β-reduction,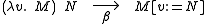
in the De Bruijn notation is, predictably,
A feature of this notation is that abstractor and applicator wagons of β-redexes are paired like parentheses. For example, consider the stages in the β-reduction of the term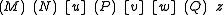
, where the redexes are underlined:
Thus, if one views the applicator as an open paren ('
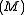can be brought to its abstractor 
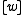, or the abstractor to the applicator. In fact, all commutatives and permutative conversions on lambda terms may be described simply in terms of parity-preserving reorderings of partnered wagons. One thus obtains a generalised conversion primitive for λ-terms in the De Bruijn notation.
Several properties of λ-terms that are difficult to state and prove using the traditional notation are easily expressed in the De Bruijn notation. For example, in a type-theoretic
setting, one can easily compute the canonical class of types for a term in a typing context, and restate the type checking problem to one of verifying that the checked type is a member of this class. De Bruijn notation has also been shown to be useful in calculi for explicit substitution
in pure type system
s.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the De Bruijn notation is a syntax for terms in the λ calculus invented by the Dutch
Netherlands
The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....
. It can be seen as a reversal of the usual syntax for the λ calculus where the argument in an application is placed next to its corresponding binder in the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
instead of after the latter's body.
Formal definition
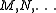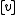Terms () in the De Bruijn notation are either variables (), or have one of two wagon prefixes. The abstractor wagon, written , corresponds to the usual λ-binder of the λ calculus, and the applicator wagon, written , corresponds to the argument in an application in the λ calculus.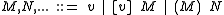Terms in the traditional syntax can be converted to the De Bruijn notation by defining an inductive function
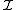for which:
All operations on λ-terms commute with respect to the
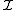translation. For example, the usual β-reduction,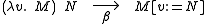in the De Bruijn notation is, predictably,
A feature of this notation is that abstractor and applicator wagons of β-redexes are paired like parentheses. For example, consider the stages in the β-reduction of the term
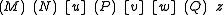, where the redexes are underlined:
Thus, if one views the applicator as an open paren ('
(') and the abstractor as a close bracket (']'), then the pattern in the above term is '((](]]'. De Bruijn called an applicator and its corresponding abstractor in this interpretation partners, and wagons without partners bachelors. A sequence of wagons, which he called a segment, is well balanced if all its wagons are partnered.Advantages of the De Bruijn notation
In a well balanced segment, the partnered wagons may be moved around arbitrarily and, as long as parity is not destroyed, the meaning of the term stays the same. For example, in the above example, the applicator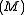 can be brought to its abstractor 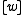, or the abstractor to the applicator. In fact, all commutatives and permutative conversions on lambda terms may be described simply in terms of parity-preserving reorderings of partnered wagons. One thus obtains a generalised conversion primitive for λ-terms in the De Bruijn notation.Several properties of λ-terms that are difficult to state and prove using the traditional notation are easily expressed in the De Bruijn notation. For example, in a type-theoretic
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
setting, one can easily compute the canonical class of types for a term in a typing context, and restate the type checking problem to one of verifying that the checked type is a member of this class. De Bruijn notation has also been shown to be useful in calculi for explicit substitution
Explicit substitution
In computer science, lambda calculi are said to have explicit substitutions if they pay special attention to the formalization of the process of substitution. This is in contrast to the standard lambda calculus where substitutions are performed by beta reductions in an implicit manner which is not...
in pure type system
Pure type system
In the branches of mathematical logic known as proof theory and type theory, a pure type system , previously known as a generalized type system , is a form of typed lambda calculus that allows an arbitrary number of sorts and dependencies between any of these...
s.