Dedekind psi function
Encyclopedia
In number theory
, the Dedekind psi function is the multiplicative function
on the positive integers defined by
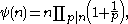
where the product is taken over all primes p dividing n (by convention, ψ(1) is the empty product
and so has value 1). The function was introduced by Richard Dedekind
in connection with modular functions.
The value of ψ(n) for the first few integers n is:
ψ(n) is greater than n for all n greater than 1, and is even for all n greater than 2. If n is a square-free number then ψ(n) = σ(n)
.
The ψ function can also be defined by setting ψ(pn) = (p+1)pn-1 for powers of any prime p, and then extending the definition to all integers by multiplicitivity. This also leads to a proof of the generating function in terms of the Riemann zeta function, which is
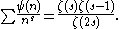
This is also a consequence of the fact that we can write as a Dirichlet convolution
of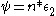
where 
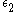is the characteristic function of the squares.
is
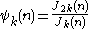
with Dirichlet series
.
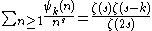It is also the Dirichlet convolution
of a power and the square
of the Mobius function
,
.
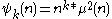If
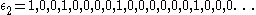
is the characteristic function of the squares, another Dirichlet convolution
leads to the generalized σ-function
,
.
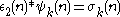Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Dedekind psi function is the multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
on the positive integers defined by
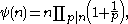
where the product is taken over all primes p dividing n (by convention, ψ(1) is the empty product
Empty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
and so has value 1). The function was introduced by Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in connection with modular functions.
The value of ψ(n) for the first few integers n is:
- 1, 3, 4, 6, 6, 12, 8, 12, 12, 18, 12, 24 ... .
ψ(n) is greater than n for all n greater than 1, and is even for all n greater than 2. If n is a square-free number then ψ(n) = σ(n)
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
.
The ψ function can also be defined by setting ψ(pn) = (p+1)pn-1 for powers of any prime p, and then extending the definition to all integers by multiplicitivity. This also leads to a proof of the generating function in terms of the Riemann zeta function, which is
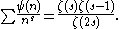
This is also a consequence of the fact that we can write as a Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
of
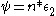where 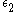is the characteristic function of the squares.Higher Orders
The generalization to higher orders via ratios of Jordan's totientJordan's totient function
In number theory, Jordan's totient function J_k of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime -tuple together with n. This is a generalisation of Euler's totient function, which is J1...
is
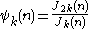
with Dirichlet series
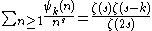.It is also the Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
of a power and the square
of the Mobius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
,
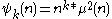.If
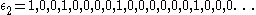
is the characteristic function of the squares, another Dirichlet convolution
leads to the generalized σ-function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
,
.
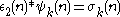