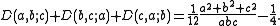Dedekind sum
Encyclopedia
In mathematics
, Dedekind sums, named after Richard Dedekind
, are certain sums of products of a sawtooth function, and are given by a function D of three integer variables. Dedekind introduced them to express the functional equation
of the Dedekind eta function
. They have subsequently been much studied in number theory
, and have occurred in some problems of topology
. Dedekind sums obey a large number of relationships on themselves; this article lists only a tiny fraction of these.
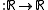as
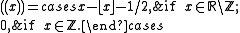
We then let
be defined by
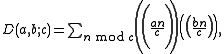
the terms on the right being the Dedekind sums. For the case a=1, one often writes
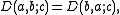
and that, by the oddness of (),
By the periodicity of D in its first two arguments, the third argument being the length of the period for both,
If d is a positive integer, then
There is a proof for the last equality making use of
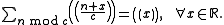
Furthermore, az = 1 (mod c) implies D(a,b;c) = D(1,bz;c).
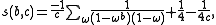
where the sum extends over the c-th roots of unity other than 1, i.e. over all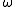
such that 
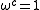and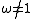 
.
If b, c > 0 are coprime, then
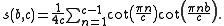
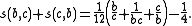
Rewriting this as
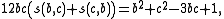
it follows that the number 6c s(b,c) is an integer.
If k = (3, c) then
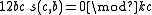
and
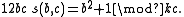
A relation that is prominent in the theory of the Dedekind eta function
is the following. Let q = 3, 5, 7 or 13 and let n = 24/(q − 1). Then given integers a, b, c, d with ad − bc = 1 (thus belonging to the modular group
), with c chosen so that c = kq for some integer k > 0, define
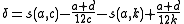
Then one has nδ is an even integer.
found the following generalization of the reciprocity law for Dedekind sums: If a,b, and c are pairwise coprime positive integers, then
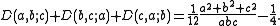
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Dedekind sums, named after Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, are certain sums of products of a sawtooth function, and are given by a function D of three integer variables. Dedekind introduced them to express the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
of the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. They have subsequently been much studied in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and have occurred in some problems of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Dedekind sums obey a large number of relationships on themselves; this article lists only a tiny fraction of these.
Definition
Define the sawtooth function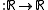 asWe then let
- D :Z3 → R
be defined by
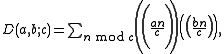
the terms on the right being the Dedekind sums. For the case a=1, one often writes
- s(b,c) = D(1,b;c).
Simple formulae
Note that D is symmetric in a and b, and hence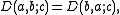and that, by the oddness of (),
- D(−a,b;c) = −D(a,b;c),
- D(a,b;−c) = D(a,b;c).
By the periodicity of D in its first two arguments, the third argument being the length of the period for both,
- D(a,b;c)=D(a+kc,b+lc;c), for all integers k,l.
If d is a positive integer, then
- D(ad,bd;cd) = dD(a,b;c),
- D(ad,bd;c) = D(a,b;c), if (d,c) = 1,
- D(ad,b;cd) = D(a,b;c), if (d,b) = 1.
There is a proof for the last equality making use of
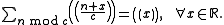
Furthermore, az = 1 (mod c) implies D(a,b;c) = D(1,bz;c).
Alternative forms
If b and c are coprime, we may write s(b,c) as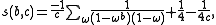where the sum extends over the c-th roots of unity other than 1, i.e. over all
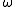such that 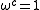and 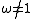.If b, c > 0 are coprime, then
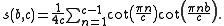
Reciprocity law
If b and c are coprime positive integers then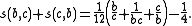Rewriting this as
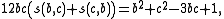
it follows that the number 6c s(b,c) is an integer.
If k = (3, c) then
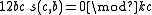
and
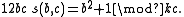
A relation that is prominent in the theory of the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
is the following. Let q = 3, 5, 7 or 13 and let n = 24/(q − 1). Then given integers a, b, c, d with ad − bc = 1 (thus belonging to the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
), with c chosen so that c = kq for some integer k > 0, define
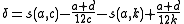
Then one has nδ is an even integer.
Rademacher's generalization of the reciprocity law
Hans RademacherHans Rademacher
Hans Adolph Rademacher was a German mathematician, known for work in mathematical analysis and number theory.-Biography:...
found the following generalization of the reciprocity law for Dedekind sums: If a,b, and c are pairwise coprime positive integers, then