
Deligne cohomology
Encyclopedia
In mathematics, Deligne cohomology is the hypercohomology of the Deligne complex of a complex manifold
. It was introduced by Pierre Deligne
in unpublished work in about 1972 as a cohomology theory for algebraic varieties that includes both ordinary cohomology and intermediate Jacobian
s.
For introductory accounts of Deligne cohomology see , , and .

where Z(p) = (2π i)pZ. Depending on the context,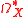 is either the complex of smooth (i.e., C∞) differential form
is either the complex of smooth (i.e., C∞) differential form
s or of holomorphic forms, respectively.
The Deligne cohomology is the q-th hypercohomology of the Deligne complex.
over X. For p = q = 2, it is the group of isomorphism classes of C×-bundles with connection. For q = 3 and p = 2 or 3, descriptions in terms of gerbe
s are available . This has been generalized to a description in higher degrees in terms of iterated classifying space
s and connections on them .
.
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
. It was introduced by Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
in unpublished work in about 1972 as a cohomology theory for algebraic varieties that includes both ordinary cohomology and intermediate Jacobian
Intermediate Jacobian
In mathematics, the intermediate Jacobian of a compact Kähler manifold or Hodge structure is a complex torus that is a common generalization of the Jacobian variety of a curve and the Picard variety and the Albanese variety. It is obtained by putting a complex structure on the torus Hn/Hn for n odd...
s.
For introductory accounts of Deligne cohomology see , , and .
Definition
The analytic Deligne complex Z(p)D, an on a complex analytic manifold X is
where Z(p) = (2π i)pZ. Depending on the context,
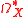 is either the complex of smooth (i.e., C∞) differential form
is either the complex of smooth (i.e., C∞) differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s or of holomorphic forms, respectively.
The Deligne cohomology is the q-th hypercohomology of the Deligne complex.
Properties
Deligne cohomology groups can be described geometrically, especially in low degrees. For p = 0, it agrees with the q-th singular cohomology group (with Z-coefficients), by definition. For q = 2 and p = 1, it is isomorphic to the group of isomorphism classes of smooth (or holomorphic, depending on the context) principal C×-bundlesPrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over X. For p = q = 2, it is the group of isomorphism classes of C×-bundles with connection. For q = 3 and p = 2 or 3, descriptions in terms of gerbe
Gerbe
In mathematics, a gerbe is a construct in homological algebra and topology. Gerbes were introduced by Jean Giraud following ideas of Alexandre Grothendieck as a tool for non-commutative cohomology in degree 2. They can be seen as a generalization of principal bundles to the setting of 2-categories...
s are available . This has been generalized to a description in higher degrees in terms of iterated classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s and connections on them .
Applications
Deligne cohomology is used to formulate Beilinson conjectures on special values of L-functionsSpecial values of L-functions
In mathematics, the study of special values of L-functions is a subfield of number theory devoted to generalising formulae such as the Leibniz formula for pi, namely...
.

