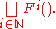Denotational semantics
Encyclopedia
In computer science
, denotational semantics (initially known as mathematical semantics or Scott–Strachey semantics) is an approach to formalizing the meanings of programming language
s by constructing mathematical objects (called denotations) which describe the meanings of expressions from the languages. Other approaches to providing a formal semantics of programming languages
include axiomatic semantics
and operational semantics
.
Broadly speaking, denotational semantics is concerned with finding mathematical objects called domains
that represent what programs do. For example, programs (or program phrases) might be represented by partial function
s, or by Actor
event diagram scenarios
, or by games between the environment and the system: these are all general examples of domains.
An important tenet of denotational semantics is that semantics should be compositional
: the denotation of a program phrase should be built out of the denotations of its subphrases
.
and Dana Scott
in the late 1960s. As originally developed by Strachey and Scott, denotational semantics provided the denotation (meaning) of a computer program as a function
that mapped input into output. To give denotations to recursively defined
programs, Scott proposed working with continuous functions between domains
, specifically complete partial order
s. As described below, work has continued in investigating appropriate denotational semantics for aspects of programming languages such as sequentiality, concurrency, non-determinism and local state.
Denotational semantics have been developed for modern programming languages that use capabilities like concurrency
and exceptions
, e.g., Concurrent ML
, CSP
, and Haskell
. The semantics of these languages is compositional in that the denotation of a phrase depends on the denotations of its subphrases. For example, the meaning of the applicative expression f(E1,E2) is defined in terms of semantics of its subphrases f, E1 and E2. In a modern programming language, E1 and E2 can be evaluated
concurrently
and the execution of one them might affect the other by interacting through shared objects
causing their denotations to be defined in terms of each other. Also, E1 or E2 might throw an exception
which could terminate
the execution of the other one. The sections below describe special cases of the semantics of these modern programming languages.
A function can be modeled as denoting a set of ordered pairs where each ordered pair in the set consists of two parts (1) an argument for the function and (2) the value of the function for that argument. For example the set of order pairs {[0 1] [4 3]} is the denotation of a function with value 1 for argument 0, value 3 for the argument 4, and is otherwise undefined.
The problem to be solved is to provide denotations for recursive programs that are defined in terms of themselves such as the definition of the factorial
function as
A solution is to build up the denotation by approximation starting with the empty set of order pairs (which in set theory would be written as {}). If {} is plugged into the above definition of factorial then the denotation is {[0 1]}, which is a better approximation of factorial. Iterating: If {[0 1]} is plugged into the definition then the denotation is {[0 1] [1 1]}. So it is convenient to think of an approximation to factorial as an input F in the following way:
It is instructive to think of a chain of "iterates" where Fi indicates i-many applications
of F.
The least upper bound of this chain is the full factorial function which can be expressed as follows where the symbol "⊔" means "least upper bound":
has been developed to give a denotational semantics to non-deterministic sequential programs
. Writing P for a power domain constructor, the domain P(D) is the domain of non-deterministic computations of type denoted by D.
There are difficulties with fairness and unboundedness
in domain-theoretic models of non-determinism. See Power domains for nondeterminism.
. For this reason various new models have been introduced. In the early 1980s, people began using the style of denotational semantics to give semantics for concurrent languages. Examples include Will Clinger's work with the actor model; Glynn Winskel's work with event structures and petri nets; and the work by Francez, Hoare, Lehmann, and de Roever (1979) on trace semantics for CSP
. All these lines of inquiry remain under investigation (see e.g. the various denotational models for CSP).
Recently, Winskel and others have proposed the category of profunctor
s as a domain theory for concurrency.
can be straightforwardly modeled in the denotational semantics described above. All the textbooks below have the details. The key idea is to consider a command as a partial function on some domain of states. The denotation of "x:=3" is then the function that takes a state to the state with 3 assigned to x. The sequencing operator ";" is denoted by composition of functions. Fixed-point constructions are then used to give a semantics to looping constructs, such as "while".
Things become more difficult in modelling programs with local variables. One approach is to no longer work with domains, but instead to interpret types as functors from some category
of worlds to a category
of domains. Programs are then denoted by natural
continuous functions between these functors.
. For example, the type of lists of numbers can be specified by
This section deals only with functional data structures that cannot change. Conventional imperative programming languages would typically allow the elements of such a recursive list to be changed.
For another example: the type of denotations of the untyped lambda calculus is
The problem of solving domain equations is concerned with finding domains that model these kinds of datatypes. One approach, roughly speaking, is to consider the collection of all domains as a domain itself, and then solve the recursive definition there. The textbooks below give more details.
Polymorphic data types are data types that are defined with a parameter. For example, the type of α lists is defined by
Lists of numbers, then, are of type Nat list, while lists of strings are of String list.
Some researchers have developed domain theoretic models of polymorphism. Other researchers have also modeled parametric polymorphism within constructive set theories. Details are found in the textbooks listed below.
A recent research area has involved denotational semantics for object and class based programming languages.
, denotational semantics have been given to languages for linear usage (see e.g. proof net
s, coherence spaces
) and also polynomial time complexity.
was, for a long time, a big open question in denotational semantics. The difficulty with PCF is that it is a very sequential language. For example, there is no way to define the parallel-or function in PCF. It is for this reason that the approach using domains, as introduced above, yields a denotational semantics that is not fully abstract.
This open question was mostly resolved in the 1990s with the development of game semantics
and also with techniques involving logical relations. For more details, see the page on PCF
.
; a high-level programming language might be translated into byte-code. (Indeed, conventional denotational semantics can be seen as the interpretation of programming languages into the internal language of the category of domains.)
In this context, notions from denotational semantics, such as full abstraction, help to satisfy security concerns.
. This is especially important when the denotational semantics is rather mathematical and abstract, and the operational semantics is more concrete or closer to the computational intuitions. The following properties of a denotational semantics are often of interest.
Additional desirable properties we may wish to hold between operational and denotational semantics are:
A basic denotational semantics in domain theory is compositional because it is given as follows. We start by considering program fragments, i.e. programs with free variables. A typing context assigns a type to each free variable. For instance, in the expression (x + y) might be considered in a typing context (x:nat,y:nat). We now give a denotational semantics to program fragments, using the following scheme.
Now, the meaning of the compound expression (7+4) is determined by composing the three functions 〚⊢7:nat〛:1→ℕ⊥, 〚⊢4:nat〛:1→ℕ⊥, and 〚x:nat,y:nat⊢x+y:nat〛:ℕ⊥×ℕ⊥→ℕ⊥.
In fact, this is a general scheme for compositional denotational semantics. There is nothing specific about domains and continuous functions here. One can work with a different category
instead. For example, in game semantics
, the category of games has games as objects and strategies as morphisms: we can interpret types as games, and programs as strategies. For a simple language without general recursion, we can make do with the category of sets and functions
. For a language with side-effects, we can work in the Kleisli category
for a monad. For a language with state, we can work in a functor category
. Milner
has advocated modelling location and interaction by working in a category with interfaces as objects and bigraphs as morphisms.
[1980]:
According to Clinger (1981):
which can be seen as a branch of model theory
, leading to connections with type theory
and category theory
. Within computer science, there are connections with abstract interpretation
, program verification, and model checking
.
Monads were introduced to denotational semantics as a way of organising semantics, and these ideas have had a big impact in functional programming
(see monads in functional programming
).
Lecture notes
Other references
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, denotational semantics (initially known as mathematical semantics or Scott–Strachey semantics) is an approach to formalizing the meanings of programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s by constructing mathematical objects (called denotations) which describe the meanings of expressions from the languages. Other approaches to providing a formal semantics of programming languages
Formal semantics of programming languages
In programming language theory, semantics is the field concerned with the rigorous mathematical study of the meaning of programming languages and models of computation...
include axiomatic semantics
Axiomatic semantics
Axiomatic semantics is an approach based on mathematical logic to proving the correctness of computer programs. It is closely related to Hoare logic....
and operational semantics
Operational semantics
In computer science, operational semantics is a way to give meaning to computer programs in a mathematically rigorous way. Operational semantics are classified into two categories: structural operational semantics formally describe how the individual steps of a computation take place in a...
.
Broadly speaking, denotational semantics is concerned with finding mathematical objects called domains
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
that represent what programs do. For example, programs (or program phrases) might be represented by partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
s, or by Actor
Actor model
In computer science, the Actor model is a mathematical model of concurrent computation that treats "actors" as the universal primitives of concurrent digital computation: in response to a message that it receives, an actor can make local decisions, create more actors, send more messages, and...
event diagram scenarios
Denotational semantics of the Actor model
The denotational semantics of the Actor model is the subject of denotational domain theory for Actors. The historical development of this subject is recounted in [Hewitt 2008b].-Actor fixed point semantics:...
, or by games between the environment and the system: these are all general examples of domains.
An important tenet of denotational semantics is that semantics should be compositional
Principle of compositionality
In mathematics, semantics, and philosophy of language, the Principle of Compositionality is the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them. This principle is also called Frege's Principle,...
: the denotation of a program phrase should be built out of the denotations of its subphrases
Phrase
In everyday speech, a phrase may refer to any group of words. In linguistics, a phrase is a group of words which form a constituent and so function as a single unit in the syntax of a sentence. A phrase is lower on the grammatical hierarchy than a clause....
.
Historical development
Denotational semantics originated in the work of Christopher StracheyChristopher Strachey
Christopher Strachey was a British computer scientist. He was one of the founders of denotational semantics, and a pioneer in programming language design...
and Dana Scott
Dana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
in the late 1960s. As originally developed by Strachey and Scott, denotational semantics provided the denotation (meaning) of a computer program as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that mapped input into output. To give denotations to recursively defined
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
programs, Scott proposed working with continuous functions between domains
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
, specifically complete partial order
Complete partial order
In mathematics, directed complete partial orders and ω-complete partial orders are special classes of partially ordered sets, characterized by particular completeness properties...
s. As described below, work has continued in investigating appropriate denotational semantics for aspects of programming languages such as sequentiality, concurrency, non-determinism and local state.
Denotational semantics have been developed for modern programming languages that use capabilities like concurrency
Concurrent computing
Concurrent computing is a form of computing in which programs are designed as collections of interacting computational processes that may be executed in parallel...
and exceptions
Exception handling
Exception handling is a programming language construct or computer hardware mechanism designed to handle the occurrence of exceptions, special conditions that change the normal flow of program execution....
, e.g., Concurrent ML
Concurrent ML
Concurrent ML is a concurrent extension of the Standard ML programming language.-Sample Code:Here is sample code to print "hello, world" to the console. It spawns a thread which creates a channel for strings. This thread then spawns another thread which prints the first string that is received...
, CSP
Communicating sequential processes
In computer science, Communicating Sequential Processes is a formal language for describing patterns of interaction in concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras, or process calculi...
, and Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
. The semantics of these languages is compositional in that the denotation of a phrase depends on the denotations of its subphrases. For example, the meaning of the applicative expression f(E1,E2) is defined in terms of semantics of its subphrases f, E1 and E2. In a modern programming language, E1 and E2 can be evaluated
Interpreter (computing)
In computer science, an interpreter normally means a computer program that executes, i.e. performs, instructions written in a programming language...
concurrently
Concurrent computing
Concurrent computing is a form of computing in which programs are designed as collections of interacting computational processes that may be executed in parallel...
and the execution of one them might affect the other by interacting through shared objects
Object (computer science)
In computer science, an object is any entity that can be manipulated by the commands of a programming language, such as a value, variable, function, or data structure...
causing their denotations to be defined in terms of each other. Also, E1 or E2 might throw an exception
Exception handling
Exception handling is a programming language construct or computer hardware mechanism designed to handle the occurrence of exceptions, special conditions that change the normal flow of program execution....
which could terminate
Abort (computing)
In a computer or data transmission system, to abort means to terminate, usually in a controlled manner, a processing activity because it is impossible or undesirable for the activity to proceed. Such an action may be accompanied by diagnostic information on the aborted process.In addition to being...
the execution of the other one. The sections below describe special cases of the semantics of these modern programming languages.
Denotations of recursive programs
A denotational semantics is given to a program phrase as a function from an environment (that has the values of its free variables) to its denotation. For example, the phrase n*m produces a denotation when provided with an environment that has binding for its two free variables: n and m. If in the environment n has the value 3 and m has the value 5, then the denotation is 15.A function can be modeled as denoting a set of ordered pairs where each ordered pair in the set consists of two parts (1) an argument for the function and (2) the value of the function for that argument. For example the set of order pairs {[0 1] [4 3]} is the denotation of a function with value 1 for argument 0, value 3 for the argument 4, and is otherwise undefined.
The problem to be solved is to provide denotations for recursive programs that are defined in terms of themselves such as the definition of the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function as
-
- factorial ≡ λ(n) if (n0) then 1 else n*factorial(n-1).
A solution is to build up the denotation by approximation starting with the empty set of order pairs (which in set theory would be written as {}). If {} is plugged into the above definition of factorial then the denotation is {[0 1]}, which is a better approximation of factorial. Iterating: If {[0 1]} is plugged into the definition then the denotation is {[0 1] [1 1]}. So it is convenient to think of an approximation to factorial as an input F in the following way:
-
- λ(F) λ(n) if (n0) then 1 else n*F(n-1).
It is instructive to think of a chain of "iterates" where Fi indicates i-many applications
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of F.
- F0({}) is the totally undefined partial function {}
- F1({}) is the function {[0 1]} that is defined at 0, to be 1, and undefined elsewhere;
- F5({}) is the function {[0 1] [1 1] [2 2] [3 6] [4 24]}
The least upper bound of this chain is the full factorial function which can be expressed as follows where the symbol "⊔" means "least upper bound":
Denotational semantics of non-deterministic programs
The concept of power domainsPower domains
In denotational semantics and domain theory, power domains are domains of nondeterministic and concurrent computations.The idea of power domains for functions is that a nondeterministic function may be described as a deterministic set-valued function, where the set contains all values the...
has been developed to give a denotational semantics to non-deterministic sequential programs
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
. Writing P for a power domain constructor, the domain P(D) is the domain of non-deterministic computations of type denoted by D.
There are difficulties with fairness and unboundedness
Unbounded nondeterminism
In computer science, unbounded nondeterminism or unbounded indeterminacy is a property of concurrency by which the amount of delay in servicing a request can become unbounded as a result of arbitration of contention for shared resources while still guaranteeing that the request will eventually be...
in domain-theoretic models of non-determinism. See Power domains for nondeterminism.
Denotational semantics of concurrency
Many researchers have argued that the domain theoretic models given above do not suffice for the more general case of concurrent computationConcurrency (computer science)
In computer science, concurrency is a property of systems in which several computations are executing simultaneously, and potentially interacting with each other...
. For this reason various new models have been introduced. In the early 1980s, people began using the style of denotational semantics to give semantics for concurrent languages. Examples include Will Clinger's work with the actor model; Glynn Winskel's work with event structures and petri nets; and the work by Francez, Hoare, Lehmann, and de Roever (1979) on trace semantics for CSP
Communicating sequential processes
In computer science, Communicating Sequential Processes is a formal language for describing patterns of interaction in concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras, or process calculi...
. All these lines of inquiry remain under investigation (see e.g. the various denotational models for CSP).
Recently, Winskel and others have proposed the category of profunctor
Profunctor
In category theory, a branch of mathematics, profunctors are a generalization of relations and also of bimodules. They are related to the notion of correspondences.- Definition :...
s as a domain theory for concurrency.
Denotational semantics of state
State (such as a heap) and simple imperative featuresImperative programming
In computer science, imperative programming is a programming paradigm that describes computation in terms of statements that change a program state...
can be straightforwardly modeled in the denotational semantics described above. All the textbooks below have the details. The key idea is to consider a command as a partial function on some domain of states. The denotation of "x:=3" is then the function that takes a state to the state with 3 assigned to x. The sequencing operator ";" is denoted by composition of functions. Fixed-point constructions are then used to give a semantics to looping constructs, such as "while".
Things become more difficult in modelling programs with local variables. One approach is to no longer work with domains, but instead to interpret types as functors from some category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of worlds to a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of domains. Programs are then denoted by natural
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
continuous functions between these functors.
Denotations of data types
Many programming languages allow users to define recursive data typesRecursive type
In computer programming languages, a recursive data type is a data type for values that may contain other values of the same type...
. For example, the type of lists of numbers can be specified by
-
- datatype list = Cons of (Nat, list) | Empty.
This section deals only with functional data structures that cannot change. Conventional imperative programming languages would typically allow the elements of such a recursive list to be changed.
For another example: the type of denotations of the untyped lambda calculus is
-
- datatype D = (D → D)
The problem of solving domain equations is concerned with finding domains that model these kinds of datatypes. One approach, roughly speaking, is to consider the collection of all domains as a domain itself, and then solve the recursive definition there. The textbooks below give more details.
Polymorphic data types are data types that are defined with a parameter. For example, the type of α lists is defined by
-
- datatype α list = Cons of (α, α list) | Empty.
Lists of numbers, then, are of type Nat list, while lists of strings are of String list.
Some researchers have developed domain theoretic models of polymorphism. Other researchers have also modeled parametric polymorphism within constructive set theories. Details are found in the textbooks listed below.
A recent research area has involved denotational semantics for object and class based programming languages.
Denotational semantics for programs of restricted complexity
Following the development of programming languages based on linear logicLinear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
, denotational semantics have been given to languages for linear usage (see e.g. proof net
Proof net
In proof theory, proof nets are a geometrical method of representing proofs thateliminates two forms of bureaucracy that differentiates proofs: irrelevant syntactical features of regular proof calculi such as the natural deduction calculus and the sequent calculus, and the order of rules applied...
s, coherence spaces
Coherent space
In proof theory, a coherent space is a concept introduced in the semantic study of linear logic.Let a set C be given. Two subsets S,T ⊆ C are said to be orthogonal, written S ⊥ T, if S ∩ T is ∅ or a singleton...
) and also polynomial time complexity.
Denotational semantics of sequentiality
The problem of full abstraction for the sequential programming language PCFProgramming language for Computable Functions
In computer science, Programming Computable Functions,"PCF is a programming language for computable functions, based on LCF, Scott’s logic of computable functions" . Programming Computable Functions is used by . It is also referred to as Programming with Computable Functions or Programming language...
was, for a long time, a big open question in denotational semantics. The difficulty with PCF is that it is a very sequential language. For example, there is no way to define the parallel-or function in PCF. It is for this reason that the approach using domains, as introduced above, yields a denotational semantics that is not fully abstract.
This open question was mostly resolved in the 1990s with the development of game semantics
Game semantics
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
and also with techniques involving logical relations. For more details, see the page on PCF
Programming language for Computable Functions
In computer science, Programming Computable Functions,"PCF is a programming language for computable functions, based on LCF, Scott’s logic of computable functions" . Programming Computable Functions is used by . It is also referred to as Programming with Computable Functions or Programming language...
.
Denotational semantics as source-to-source translation
It is often useful to translate one programming language into another. For example, a concurrent programming language might be translated into a process calculusProcess calculus
In computer science, the process calculi are a diverse family of related approaches for formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes...
; a high-level programming language might be translated into byte-code. (Indeed, conventional denotational semantics can be seen as the interpretation of programming languages into the internal language of the category of domains.)
In this context, notions from denotational semantics, such as full abstraction, help to satisfy security concerns.
Abstraction
It is often considered important to connect denotational semantics with operational semanticsOperational semantics
In computer science, operational semantics is a way to give meaning to computer programs in a mathematically rigorous way. Operational semantics are classified into two categories: structural operational semantics formally describe how the individual steps of a computation take place in a...
. This is especially important when the denotational semantics is rather mathematical and abstract, and the operational semantics is more concrete or closer to the computational intuitions. The following properties of a denotational semantics are often of interest.
- Syntax independence: The denotations of programs should not involve the syntax of the source language.
- Soundness: All observably distinctObservational equivalenceIn econometrics, two parameter values are considered observationally equivalent if they both result in the same probability distribution of observable data...
programs have distinct denotations; - Full abstraction: Two programs have the same denotations precisely when they are observationally equivalentObservational equivalenceIn econometrics, two parameter values are considered observationally equivalent if they both result in the same probability distribution of observable data...
. For semantics in the traditional style, full abstraction may be understood roughly as the requirement that "operational equivalence coincides with denotational equality". For denotational semantics in more intensional models, such as the Actor modelActor modelIn computer science, the Actor model is a mathematical model of concurrent computation that treats "actors" as the universal primitives of concurrent digital computation: in response to a message that it receives, an actor can make local decisions, create more actors, send more messages, and...
and process calculi, there are different notions of equivalence within each model, and so the concept of full abstraction is a matter of debate, and harder to pin down. Also the mathematical structure of operational semantics and denotational semantics can become very close.
Additional desirable properties we may wish to hold between operational and denotational semantics are:
- Constructivism: ConstructivismConstructivism (mathematics)In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
is concerned with whether domain elements can be shown to exist by constructive methods. - Independence of denotational and operational semantics: The denotational semantics should be formalized using mathematical structures that are independent of the operational semantics of a programming language; However, the underlying concepts can be closely related. See the section on Compositionality below.
- Full completeness or definability: Every morphism of the semantic model should be the denotation of a program.
Compositionality
An important aspect of denotational semantics of programming languages is compositionality, by which the denotation of a program is constructed from denotations of its parts. For example consider the expression "7 + 4". Compositionality in this case is to provide a meaning for "7 + 4" in terms of the meanings of "7", "4" and "+".A basic denotational semantics in domain theory is compositional because it is given as follows. We start by considering program fragments, i.e. programs with free variables. A typing context assigns a type to each free variable. For instance, in the expression (x + y) might be considered in a typing context (x:nat,y:nat). We now give a denotational semantics to program fragments, using the following scheme.
- We begin by describing the meaning of the types of our language: the meaning of each type must be a domain. We write 〚τ〛 for the domain denoting the type τ. For instance, the meaning of type nat should be the domain of natural numbers: 〚nat〛=ℕ⊥.
- From the meaning of types we derive a meaning for typing contexts. We set 〚 x1:τ1,..., xn:τn〛 = 〚 τ1〛× ... ×〚τn〛. For instance, 〚x:nat,y:nat〛= ℕ⊥×ℕ⊥. As a special case, the meaning of the empty typing context, with no variables, is the domain with one element, denoted 1.
- Finally, we must give a meaning to each program-fragment-in-typing-context. Suppose that P is a program fragment of type σ, in typing context Γ, often written Γ⊢P:σ. Then the meaning of this program-in-typing-context must be a continuous function 〚Γ⊢P:σ〛:〚Γ〛→〚σ〛. For instance, 〚⊢7:nat〛:1→ℕ⊥ is the constantly "7" function, while 〚x:nat,y:nat⊢x+y:nat〛:ℕ⊥×ℕ⊥→ℕ⊥ is the function that adds two numbers.
Now, the meaning of the compound expression (7+4) is determined by composing the three functions 〚⊢7:nat〛:1→ℕ⊥, 〚⊢4:nat〛:1→ℕ⊥, and 〚x:nat,y:nat⊢x+y:nat〛:ℕ⊥×ℕ⊥→ℕ⊥.
In fact, this is a general scheme for compositional denotational semantics. There is nothing specific about domains and continuous functions here. One can work with a different category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
instead. For example, in game semantics
Game semantics
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. In the late 1950s Paul Lorenzen was the...
, the category of games has games as objects and strategies as morphisms: we can interpret types as games, and programs as strategies. For a simple language without general recursion, we can make do with the category of sets and functions
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. For a language with side-effects, we can work in the Kleisli category
Kleisli category
In category theory, a Kleisli category is a category naturally associated to any monad T. It is equivalent to the category of free T-algebras. The Kleisli category is one of two extremal solutions to the question Does every monad arise from an adjunction? The other extremal solution is the...
for a monad. For a language with state, we can work in a functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
. Milner
Robin Milner
Arthur John Robin Gorell Milner FRS FRSE was a prominent British computer scientist.-Life, education and career:...
has advocated modelling location and interaction by working in a category with interfaces as objects and bigraphs as morphisms.
Semantics versus implementation
According to Dana ScottDana Scott
Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...
[1980]:
- It is not necessary for the semantics to determine an implementation, but it should provide criteria for showing that an implementation is correct.
According to Clinger (1981):
- Usually, however, the formal semantics of a conventional sequential programming language may itself be interpreted to provide an (inefficient) implementation of the language. A formal semantics need not always provide such an implementation, though, and to believe that semantics must provide an implementation leads to confusion about the formal semantics of concurrent languages. Such confusion is painfully evident when the presence of unbounded nondeterminism in a programming language's semantics is said to imply that the programming language cannot be implemented.
Connections to other areas of computer science
Some work in denotational semantics has interpreted types as domains in the sense of domain theoryDomain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
which can be seen as a branch of model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, leading to connections with type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. Within computer science, there are connections with abstract interpretation
Abstract interpretation
In computer science, abstract interpretation is a theory of sound approximation of the semantics of computer programs, based on monotonic functions over ordered sets, especially lattices. It can be viewed as a partial execution of a computer program which gains information about its semantics In...
, program verification, and model checking
Model checking
In computer science, model checking refers to the following problem:Given a model of a system, test automatically whether this model meets a given specification....
.
Monads were introduced to denotational semantics as a way of organising semantics, and these ideas have had a big impact in functional programming
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
(see monads in functional programming
Monads in functional programming
In functional programming, a monad is a programming structure that represents computations. Monads are a kind of abstract data type constructor that encapsulate program logic instead of data in the domain model...
).
Further reading
Textbooks- Joseph E. StoyJoe StoyJoseph E. "Joe" Stoy is a British computer scientist. He originally studied physics at Oxford University. Early in his career, in the 1970s, he worked on denotational semantics with Christopher Strachey in the Programming Research Group at the Oxford University Computing Laboratory. He was a Fellow...
, Denotational Semantics: The Scott-Strachey Approach to Programming Language Semantics. MIT PressMIT PressThe MIT Press is a university press affiliated with the Massachusetts Institute of Technology in Cambridge, Massachusetts .-History:...
, Cambridge, Massachusetts, 1977. (A classic if dated textbook.) - Carl Gunter, "Semantics of Programming Languages: Structures and Techniques". MIT PressMIT PressThe MIT Press is a university press affiliated with the Massachusetts Institute of Technology in Cambridge, Massachusetts .-History:...
, Cambridge, Massachusetts, 1992. (ISBN 978-0262071437) - Glynn Winskel, Formal Semantics of Programming Languages. MIT PressMIT PressThe MIT Press is a university press affiliated with the Massachusetts Institute of Technology in Cambridge, Massachusetts .-History:...
, Cambridge, Massachusetts, 1993. (ISBN 978-0262731034) - R. D. Tennent, Denotational semantics. Handbook of logic in computer science, vol. 3 pp 169–322. Oxford University Press, 1994. (ISBN 0-19-853762-X)
- S. Abramsky and A. Jung: Domain theory. In S. Abramsky, D. M. Gabbay, T. S. E. Maibaum, editors, Handbook of Logic in Computer Science, vol. III. Oxford University PressOxford University PressOxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
, 1994. (ISBN 0-19-853762-X) - David A. Schmidt, Denotational semantics: a methodology for language development, Allyn and Bacon, 1986, ISBN 0205104509 (out or print now; free electronic version available)
Lecture notes
- Glynn Winskel. Denotational Semantics. University of Cambridge.
Other references
- Irene Greif. Semantics of Communicating Parallel Processes MIT EECS Doctoral Dissertation. August 1975.
- Gordon PlotkinGordon PlotkinGordon D. Plotkin, FRS, FRSE is a Scottish computer scientist.Gordon Plotkin is best-known for his introduction of structural operational semantics and his work on denotational semantics. In particular, his notes on A Structural Approach to Operational Semantics of 1981 were very influential...
. A powerdomain construction SIAM Journal on ComputingSIAM Journal on ComputingThe SIAM Journal on Computing is a scientific journal focusing on the mathematical and formal aspects of computer science. It is published by the Society for Industrial and Applied Mathematics . As of September 2008, Éva Tardos serves as editor-in-chief.-External links:** on DBLP...
September 1976. - Edsger DijkstraEdsger DijkstraEdsger Wybe Dijkstra ; ) was a Dutch computer scientist. He received the 1972 Turing Award for fundamental contributions to developing programming languages, and was the Schlumberger Centennial Chair of Computer Sciences at The University of Texas at Austin from 1984 until 2000.Shortly before his...
. A Discipline of Programming Prentice HallPrentice HallPrentice Hall is a major educational publisher. It is an imprint of Pearson Education, Inc., based in Upper Saddle River, New Jersey, USA. Prentice Hall publishes print and digital content for the 6-12 and higher-education market. Prentice Hall distributes its technical titles through the Safari...
. 1976. - Krzysztof R. Apt, J. W. de Bakker. Exercises in Denotational Semantics MFCS 1976: 1-11
- J. W. de Bakker. Least Fixed Points Revisited Theoretical Computer ScienceTheoretical Computer Science (journal)Theoretical Computer Science is a computer science journal published by Elsevier, started in 1975 and covering theoretical computer science. The journal publishes 52 issues a year. It is abstracted and indexed by Scopus and the Science Citation Index...
2(2): 155-181 (1976) - Carl HewittCarl HewittCarl Hewitt is Board Chair of the International Society for Inconsistency Robustness. He has been a Visiting Professor at Stanford University and the University of Keio. In 2000, he became emeritus in the EECS department at MIT....
and Henry Baker Actors and Continuous Functionals Proceeding of IFIP Working Conference on Formal Description of Programming Concepts. August 1–5, 1977. - Henry BakerHenry Baker (computer scientist)Henry Givens Baker Jr. is a computer scientist who has made contributions in garbage collection, functional programming languages, and linear logic. He was also one of the founders of Symbolics...
. Actor Systems for Real-Time Computation MIT EECS Doctoral Dissertation. January 1978. - Michael Smyth. Power domains Journal of Computer and System SciencesJournal of Computer and System SciencesThe Journal of Computer and System Sciences is a peer-reviewed scientific journal journal in the field of computer science. JCSS is published by Elsevier, and it was started in 1967. Many influential scientific articles have been published in JCSS; these include four papers that have won the Gödel...
. 1978. - George Milne and Robin MilnerRobin MilnerArthur John Robin Gorell Milner FRS FRSE was a prominent British computer scientist.-Life, education and career:...
. Concurrent processes and their syntax JACM. April, 1979. - Nissim Francez, C.A.R. Hoare, Daniel Lehmann, and Willem-Paul de Roever. Semantics of nondeterminism, concurrency, and communication Journal of Computer and System Sciences. December 1979.
- Nancy LynchNancy LynchNancy Ann Lynch is a professor at the Massachusetts Institute of Technology. She is the NEC Professor of Software Science and Engineering in the EECS department and heads the Theory of Distributed Systems research group at MIT's Computer Science and Artificial Intelligence Laboratory.She is the...
and Michael J. FischerMichael J. FischerMichael John Fischer is a computer scientist who works in the fields of distributed computing, parallel computing, cryptography, algorithms and data structures, and computational complexity.-Career:...
. On describing the behavior of distributed systems in Semantics of Concurrent Computation. Springer-VerlagSpringer Science+Business Media- Selected publications :* Encyclopaedia of Mathematics* Ergebnisse der Mathematik und ihrer Grenzgebiete * Graduate Texts in Mathematics * Grothendieck's Séminaire de géométrie algébrique...
. 1979. - Jerald Schwartz Denotational semantics of parallelism in Semantics of Concurrent Computation. Springer-Verlag. 1979.
- William Wadge. An extensional treatment of dataflow deadlock Semantics of Concurrent Computation. Springer-Verlag. 1979.
- Ralph-Johan BackRalph-Johan BackRalph-Johan Back is a Finnish computer scientist.Back originated the refinement calculus, an important approach to the formal development of programs using stepwise refinement, in his 1978 PhD thesis at the University of Helsinki, On the Correctness of Refinement Steps in Program Development. He...
. Semantics of Unbounded Nondeterminism ICALP 1980. - David Park. On the semantics of fair parallelism Proceedings of the Winter School on Formal Software Specification. Springer-Verlag. 1980.
- Will Clinger, of Actor Semantics. MIT Mathematics Doctoral Dissertation, June 1981.
- Lloyd Allison, A Practical Introduction to Denotational Semantics Cambridge University PressCambridge University PressCambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
. 1987. - P. America, J. de Bakker, J. N. Kok and J. Rutten. Denotational semantics of a parallel object-oriented language Information and Computation, 83(2):152–205 (1989)
- David A. Schmidt, The Structure of Typed Programming Languages. MIT Press, Cambridge, Massachusetts, 1994. ISBN 0-262-69171-X.
- M. Korff True concurrency semantics for single pushout graph transformations with applications to actor systems Working papers of the Int. Workshop on Information Systems - Correctness and Reusability. World Scientific. 1995.
- M. Korff and L. Ribeiro Concurrent derivations as single pushout graph grammar processes Proceedings of the Joint COMPUGRAPH/SEMAGRAPH Workshop on Graph Rewriting and Computation. ENTCS Vol 2, Elsevier. 1995.
- Thati, Prasanna, Carolyn Talcott, and Gul Agha. Techniques for Executing and Reasoning About Specification Diagrams International Conference on Algebraic Methodology and Software Technology (AMAST), 2004.
- J.C.M. Baeten, T. Basten, and M.A. Reniers. Algebra of Communicating Processes Cambridge University Press. 2005.
- He JifengHe JifengHe Jifeng is a Chinese computer scientist.He Jifeng was a Senior Research Fellow at the Programming Research Group in the Oxford University Computing Laboratory from 1984 to 1998. He worked extensively on formal aspects of computing science...
and C.A.R. Hoare. Linking Theories of Concurrency United Nations University International Institute for Software Technology UNU-IIST Report No. 328. July, 2005. - Luca Aceto and Andrew D. Gordon (editors). Algebraic Process Calculi: The First Twenty Five Years and Beyond Process Algebra. Bertinoro, Forlì, Italy, August 1–5, 2005.
- A. W. RoscoeBill RoscoeA. William "Bill" Roscoe is a Scottish computer scientist. He is Head of the Department of Computer Science, University of Oxford and a Professor of Computing Science...
. The Theory and Practice of Concurrency, Prentice HallPrentice HallPrentice Hall is a major educational publisher. It is an imprint of Pearson Education, Inc., based in Upper Saddle River, New Jersey, USA. Prentice Hall publishes print and digital content for the 6-12 and higher-education market. Prentice Hall distributes its technical titles through the Safari...
, ISBN 0-13-674409-5. Revised 2005.
External links
- Denotational Semantics. Overview of book by Lloyd Allison
- Structure of Programming Languages I: Denotational Semantics. Course notes from 1995 by Wolfgang Schreiner