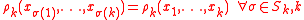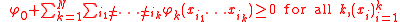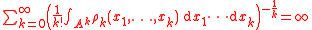Determinantal point process
Encyclopedia
In mathematics
, a determinantal point process is a stochastic
point process
, the probability distribution of which is characterized as a determinant
of some function. Such processes arise as important tools in random matrix
theory, combinatorics
, and physics
.
be a locally compact Polish space
and
be a Radon measure on 
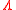. Also, consider a measurable function K:Λ2 → ℂ.
We say that
is a determinantal point process on 
with kernel 
if it is a simple point process on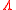 
with joint intensities given by
for every n ≥ 1 and x1, . . . , xn ∈ Λ.
for every bounded Borel A ⊆ Λ.
with kernel
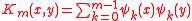
where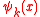
is the 
th oscillator wave function defined by
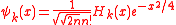
and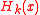
is the 
th Hermite polynomial
.
of integers (and therefore on Young diagrams) plays an important role in the study of the longest increasing subsequence
of a random permutation. The point process corresponding to a random Young diagram, expressed in modified Frobenius coordinates, is a determinantal point process on ℤ + with the discrete Bessel kernel, given by:
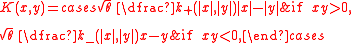
where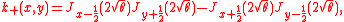
For J the Bessel function
of the first kind, and θ the mean used in poissonization.
This serves as an example of a well-defined determinantal point process with non-Hermitian kernel (although its restriction to the positive and negative semi-axis is Hermitian).
, with edge set E. Define Ie:E → ℓ2(E) as follows: first choose some arbitrary set of orientations for the edges E, and for each resulting, oriented edge e, define Ie to be the projection of a unit flow along e onto the subspace of ℓ2(E) spanned by star flows. Then the uniformly random spanning tree of G is a determinantal point process on E, with kernel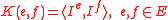
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a determinantal point process is a stochastic
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
point process
Point process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
, the probability distribution of which is characterized as a determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of some function. Such processes arise as important tools in random matrix
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
theory, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
Definition
Let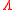 be a locally compact Polish spacePolish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
and
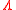be a Radon measure on . Also, consider a measurable function K:Λ2 → ℂ.We say that
is a determinantal point process on with kernel if it is a simple point process on 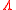with joint intensities given byfor every n ≥ 1 and x1, . . . , xn ∈ Λ.
Existence
The following two conditions are necessary and sufficient for the existence of a determinantal random point process with intensities ρk.- Symmetry: ρk is invariant under action of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sk. Thus:
- Positivity: For any N, and any collection of measurable, bounded functions φk:Λk → ℝ, k = 1,. . . ,N with compact support:
- If
- Then
Uniqueness
A sufficient condition for the uniqueness of a determinantal random process with joint intensities ρk is
for every bounded Borel A ⊆ Λ.
Gaussian unitary ensemble
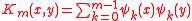
The eigenvalues of a random m × m Hermitian matrix drawn from the Gaussian unitary ensemble (GUE) form a determinantal point process on with kernelwhere
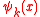is the th oscillator wave function defined by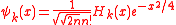and
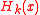is the th Hermite polynomialHermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
.
Poissonized Plancherel measure
The poissonized Plancherel measure on partitionsPartition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of integers (and therefore on Young diagrams) plays an important role in the study of the longest increasing subsequence
Longest increasing subsequence
The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible...
of a random permutation. The point process corresponding to a random Young diagram, expressed in modified Frobenius coordinates, is a determinantal point process on ℤ + with the discrete Bessel kernel, given by:
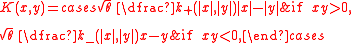
where
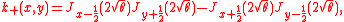
For J the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind, and θ the mean used in poissonization.
This serves as an example of a well-defined determinantal point process with non-Hermitian kernel (although its restriction to the positive and negative semi-axis is Hermitian).
Uniform spanning trees
Let G be a finite, undirected, connected graphGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, with edge set E. Define Ie:E → ℓ2(E) as follows: first choose some arbitrary set of orientations for the edges E, and for each resulting, oriented edge e, define Ie to be the projection of a unit flow along e onto the subspace of ℓ2(E) spanned by star flows. Then the uniformly random spanning tree of G is a determinantal point process on E, with kernel
.
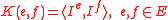