Differential evolution
Encyclopedia
In computer science
, differential evolution (DE) is a method that optimizes
a problem by iteratively
trying to improve a candidate solution
with regard to a given measure of quality. Such methods are commonly known as metaheuristic
s as they make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics such as DE do not guarantee an optimal solution is ever found.
DE is used for multidimensional real-valued functions
but does not use the gradient
of the problem being optimized, which means DE does not require for the optimization problem to be differentiable as is required by classic optimization methods such as gradient descent
and quasi-newton methods. DE can therefore also be used on optimization problems that are not even continuous, are noisy, change over time, etc.
DE optimizes a problem by maintaining a population of candidate solutions and creating new candidate solutions by combining existing ones according to its simple formulae, and then keeping whichever candidate solution has the best score or fitness on the optimization problem at hand. In this way the optimization problem is treated as a black box that merely provides a measure of quality given a candidate solution and the gradient is therefore not needed.
DE is originally due to Storn and Price. Books have been published on theoretical and practical aspects of using DE in parallel computing
, multiobjective optimization
, constrained optimization, and the books also contain surveys of application areas .
e to combine the positions of existing agents from the population. If the new position of an agent is an improvement it is accepted and forms part of the population, otherwise the new position is simply discarded. The process is repeated and by doing so it is hoped, but not guaranteed, that a satisfactory solution will eventually be discovered.
Formally, let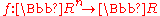
be the cost function which must be minimized or fitness function which must be maximized. The function takes a candidate solution as argument in the form of a vector of real number
s and produces a real number as output which indicates the fitness of the given candidate solution. The gradient
of
is not known. The goal is to find a solution 
for which 
for all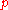 
in the search-space, which would mean 
is the global minimum. Maximization can be performed by considering the function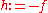 
instead.
Let
designate a candidate solution (agent) in the population. The basic DE algorithm can then be described as follows:
Note that
is called the differential weight and 
is called the crossover probability, both these parameters are selectable by the practitioner along with the population size 
see below.
and 
can have a large impact on optimization performance. Selecting the DE parameters that yield good performance has therefore been the subject of much research. Rules of thumb for parameter selection were devised by Storn et al. and Liu and Lampinen . Mathematical convergence analysis regarding parameter selection was done by Zaharie . Meta-optimization
of the DE parameters was done by Pedersen and Zhang et al..
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, differential evolution (DE) is a method that optimizes
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
a problem by iteratively
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
trying to improve a candidate solution
Candidate solution
In optimization , a candidate solution is a member of a set of possible solutions to a given problem. A candidate solution does not have to be a likely or reasonable solution to the problem – it is simply in the set that satisfies all constraints.The space of all candidate solutions is called the...
with regard to a given measure of quality. Such methods are commonly known as metaheuristic
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
s as they make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics such as DE do not guarantee an optimal solution is ever found.
DE is used for multidimensional real-valued functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
but does not use the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the problem being optimized, which means DE does not require for the optimization problem to be differentiable as is required by classic optimization methods such as gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
and quasi-newton methods. DE can therefore also be used on optimization problems that are not even continuous, are noisy, change over time, etc.
DE optimizes a problem by maintaining a population of candidate solutions and creating new candidate solutions by combining existing ones according to its simple formulae, and then keeping whichever candidate solution has the best score or fitness on the optimization problem at hand. In this way the optimization problem is treated as a black box that merely provides a measure of quality given a candidate solution and the gradient is therefore not needed.
DE is originally due to Storn and Price. Books have been published on theoretical and practical aspects of using DE in parallel computing
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
, multiobjective optimization
Multiobjective optimization
Multi-objective optimization , also known as multi-criteria or multi-attribute optimization, is the process of simultaneously optimizing two or more conflicting objectives subject to certain constraints....
, constrained optimization, and the books also contain surveys of application areas .
Algorithm
A basic variant of the DE algorithm works by having a population of candidate solutions (called agents). These agents are moved around in the search-space by using simple mathematical formulaFormula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
e to combine the positions of existing agents from the population. If the new position of an agent is an improvement it is accepted and forms part of the population, otherwise the new position is simply discarded. The process is repeated and by doing so it is hoped, but not guaranteed, that a satisfactory solution will eventually be discovered.
Formally, let
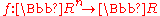be the cost function which must be minimized or fitness function which must be maximized. The function takes a candidate solution as argument in the form of a vector of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and produces a real number as output which indicates the fitness of the given candidate solution. The gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
is not known. The goal is to find a solution for which for all 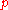in the search-space, which would mean is the global minimum. Maximization can be performed by considering the function 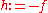instead.Let
designate a candidate solution (agent) in the population. The basic DE algorithm can then be described as follows:- Initialize all agents
with random positions in the search-space. - Until a termination criterion is met (e.g. number of iterations performed, or adequate fitness reached), repeat the following:
- For each agent
in the population do:
- Pick three agents
, and 
from the population at random, they must be distinct from each other as well as from agent 
- Pick a random index
(
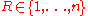being the dimensionality of the problem to be optimized). - Compute the agent's potentially new position
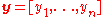as follows:
- Pick a uniformly distributed number
- If
or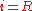 
then set 
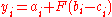otherwise set 
- Pick a uniformly distributed number
- If
then replace the agent in the population with the improved candidate solution, that is, replace 
with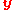 
in the population.
- Pick three agents
- For each agent
- Pick the agent from the population that has the highest fitness or lowest cost and return it as the best found candidate solution.
Note that
is called the differential weight and is called the crossover probability, both these parameters are selectable by the practitioner along with the population size see below.Parameter selection
The choice of DE parameters and can have a large impact on optimization performance. Selecting the DE parameters that yield good performance has therefore been the subject of much research. Rules of thumb for parameter selection were devised by Storn et al. and Liu and Lampinen . Mathematical convergence analysis regarding parameter selection was done by Zaharie . Meta-optimizationMeta-optimization
In numerical optimization, meta-optimization is the use of one optimization method to tune another optimization method. Meta-optimization is reported to have been used as early as in the late 1970s by Mercer and Sampson for finding optimal parameter settings of a genetic algorithm...
of the DE parameters was done by Pedersen and Zhang et al..
Variants
Variants of the DE algorithm are continually being developed in an effort to improve optimization performance. Many different schemes for performing crossover and mutation of agents are possible in the basic algorithm given above, see e.g.. More advanced DE variants are also being developed with a popular research trend being to perturb or adapt the DE parameters during optimization, see e.g. Price et al., Liu and Lampinen , Qin and Suganthan , and Brest et al..External links
- Storn's Homepage on DE featuring source-code for several programming languages.