Differential ideal
Encyclopedia
In the theory of differential form
s, a differential ideal I is an algebraic ideal in the ring of smooth differential forms on a smooth manifold, in other words a graded ideal
in the sense of ring theory
, that is further closed under exterior differentiation d. In other words, for any form α in I, the exterior derivative dα is also in I.
In the theory of differential algebra
, a differential ideal I in a differential ring R is an ideal which is mapped to itself by each differential operator.
.
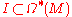One can express any partial differential equation
system as an exterior differential system with independence condition. Say that we have kth order partial differential equation systems for maps
, given by
.
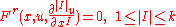The solution of this partial differential equation system is the submanifold
of the jet space
consisting of integral manifolds of the pullback of the contact system
to
.
This idea allows one to analyze the properties of partial differential equations with methods of differential geometry. For instance, we can apply Cartan's method on partial differential equation systems by writing down the exterior differential system associated with it.
which has the property that if it contains an element 
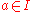they contain any element 
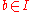such that 
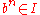for some 
is equal to 
.
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, a differential ideal I is an algebraic ideal in the ring of smooth differential forms on a smooth manifold, in other words a graded ideal
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
in the sense of ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, that is further closed under exterior differentiation d. In other words, for any form α in I, the exterior derivative dα is also in I.
In the theory of differential algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
, a differential ideal I in a differential ring R is an ideal which is mapped to itself by each differential operator.
Exterior differential systems and partial differential equations
An exterior differential system on a manifold M is a differential ideal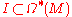.One can express any partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
system as an exterior differential system with independence condition. Say that we have kth order partial differential equation systems for maps
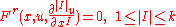, given by.The solution of this partial differential equation system is the submanifold
of the jet spaceJet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
consisting of integral manifolds of the pullback of the contact system
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
to
.This idea allows one to analyze the properties of partial differential equations with methods of differential geometry. For instance, we can apply Cartan's method on partial differential equation systems by writing down the exterior differential system associated with it.
Perfect differential ideals
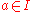a differential ideal which has the property that if it contains an element they contain any element 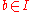such that 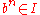for some is equal to .