Differential privacy
Encyclopedia
Differential privacy aims to provide means to maximize the accuracy of queries from statistical databases while minimizing the chances of identifying its records.
.
The notion of indistinguishability, later termed Differential Privacy, formalizes the notion of "privacy" in statistical databases.
algorithm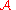
.
A randomized algorithm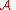
gives
-differential privacy if, when
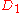and
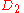are drawn at random from the pairs of datasets that differ on a single element
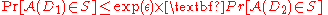
for all
,
where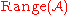
denotes the output range of the algorithm 
.
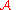N.B.: Differential Privacy is a condition on the release mechanism and not on the dataset.
This means that for any two datasets which are close to one another (that is, which differ on a single element) a given differentially private algorithm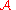
will behave approximately same on both data sets. The definition gives a strong guarantee that presence or absence of an individual will not affect the final output of the query significantly.
For example, assume we have a database of medical records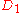
where each record is a pair (Name,X), where 
denotes whether a person has diabetes or not. For example:
Now suppose a malicious user (often termed an adversary) wants to find whether Chandler has diabetes or not. As a side information he knows in which row of the database Chandler resides. Now suppose the adversary is only allowed to use a particular form of query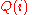
which returns the partial sum of first 
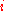rows of column 
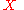in the database. In order to find Chandler's diabetes status the adversary simply executes 
. One striking feature this example highlights is: individual information can be compromised even without explicitly querying for the specific individual information.
Let us take this example a little further. Now we construct
by replacing (Chandler,1) with (Chandler,0). Let us
call the release mechanism (which releases the output of
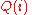) as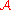 
. We say
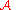is 
-differentially
private if it satisfies the definition, where
can be thought of as a singleton
set (something like
etc.) if the output
function of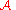
is a Discrete Random Variable
(i.e. has a probability mass function(pmf)); else if it is a
Continuous Random Variable (i.e. has a probability density
function(pdf)), then
can be thought to be a small
range of reals (something like
).
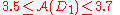In essence if such an
exist then a particular
individual's presence or absence in the database will not alter the
distribution of the output of the query by a significant amount and
thus assures privacy of individual information in an information
theoretic sense.
and the Massachusetts Group Insurance Commission (GIC) medical encounter
database.
has offered $1,000,000 prize for a 10% improvement in its recommendation system. Netflix has also released a training dataset for the competing developers to train their systems. While releasing this dataset they had provided a disclaimer: To protect customer privacy, all personal information identifying individual customers has been removed and all customer ids have been replaced by randomly-assigned ids.
Netflix is not the only available movie rating portal on the web; there are many including IMDB. In IMDB also individuals can register and rate movies, moreover they have the option of not keeping their details anonymous. Narayanan and Shmatikov had cleverly linked the Netflix anonymized training database with the Imdb database (using the date of rating by a user) to partly de-anonymize the Netflix training database. Thus clearly the individual information of a user was compromised.
the sensitivity (
) of a function 
is
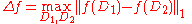
for all
,
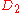differing in at most one element, and 
.
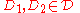To get more intuition into this let us return to the example of the medical database and a query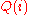
(which can also be seen as the function 
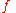) to find how many people in the first 
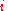rows of the database have diabetes. Clearly, if we change one of the entries in the database then the output of the query 
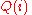will change by at most one. So, the sensitivity of this query is one. It so happens that there are techniques(which we will describe below) using which we can create a differentially private algorithm for functions with low sensitivity.
, mean zero and standard deviation 
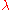). Now in our case we define the output function of 
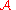as a real valued function (called as the transcript output by 
) 
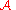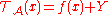, where 
and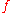 
is the original real valued query/function we plan to execute on the database. Now clearly 
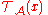can be considered to be a continuous random variable, where
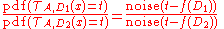
which is atmost
. We can consider 
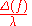to be the privacy factor 
. Thus 
follows a differentially private mechanism (as can be seen from the definition). If we try to use this concept in our diabetes example then it follows from the above derived fact that in order to have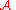 
as the 
-differential private algorithm we need to have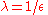 
.
Though we have used Laplacian noise here but we can use other forms of noises which also allows to create a differentially private mechanism, such as the Gaussian Noise (where of course a slight relaxation of the definition of differential privacy is needed).
times, the result would be 
-differentially private.
More generally if there is mechanisms
which are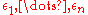 
differentially private, respectively, then any function of them 
is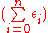 
-differentially private.
rows, which amounts to adversary with arbitrary auxiliary information can know if 
particular participants submitted their information. This can be achieved because if 
items change, the probability dilation is bounded by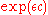 
instead of 
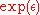, i.e. for D1 and D2 differing on 
items:
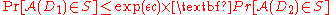
Thus setting ε instead to
achieves the desired result (protection of 
items). In other words, instead of having each item ε-differentially private protected, now every group of 
items is ε-differentially private protected (and each item is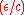 
-differentially private protected).
:
,
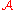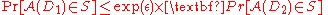and
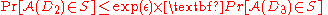
hence:
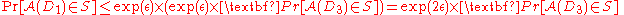
The proof can be extended to
instead of 2.
– a technique for designing differentially private algorithms
Situation
Consider a trusted party that holds a dataset of sensitive information (e.g. medical records, voter registration information, email usage) with the goal of providing global, statistical information about the data publicly available, while preserving the privacy of the users whose information the data set contains. Such a system is called a statistical databaseStatistical database
A statistical database is a database used for statistical analysis purposes. It is an OLAP instead of OLTP system, although this term precedes that modern decision, and classical statistical databases are often closer to the relational model than the multidimensional model commonly used in OLAP...
.
The notion of indistinguishability, later termed Differential Privacy, formalizes the notion of "privacy" in statistical databases.
ε-differential privacy
The actions of the trusted server are modeled via a randomizedalgorithm
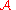.A randomized algorithm
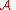gives-differential privacy if, when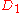 and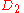 are drawn at random from the pairs of datasets that differ on a single element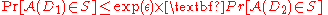for all
,where
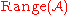denotes the output range of the algorithm 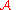.N.B.: Differential Privacy is a condition on the release mechanism and not on the dataset.
This means that for any two datasets which are close to one another (that is, which differ on a single element) a given differentially private algorithm
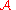will behave approximately same on both data sets. The definition gives a strong guarantee that presence or absence of an individual will not affect the final output of the query significantly.For example, assume we have a database of medical records
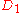where each record is a pair (Name,X), where denotes whether a person has diabetes or not. For example:| Name | Has Diabetes (X) |
|---|---|
| Ross | 1 |
| Monica | 1 |
| Joey | 0 |
| Phoebe | 0 |
| Chandler | 1 |
Now suppose a malicious user (often termed an adversary) wants to find whether Chandler has diabetes or not. As a side information he knows in which row of the database Chandler resides. Now suppose the adversary is only allowed to use a particular form of query
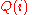which returns the partial sum of first 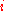rows of column 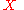in the database. In order to find Chandler's diabetes status the adversary simply executes . One striking feature this example highlights is: individual information can be compromised even without explicitly querying for the specific individual information.Let us take this example a little further. Now we construct
by replacing (Chandler,1) with (Chandler,0). Let uscall the release mechanism (which releases the output of
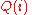) as 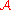. We say 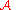is -differentiallyprivate if it satisfies the definition, where
can be thought of as a singletonset (something like
etc.) if the outputfunction of
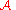is a Discrete Random Variable(i.e. has a probability mass function(pmf)); else if it is a
Continuous Random Variable (i.e. has a probability density
function(pdf)), then
can be thought to be a smallrange of reals (something like
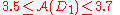).In essence if such an
exist then a particularindividual's presence or absence in the database will not alter the
distribution of the output of the query by a significant amount and
thus assures privacy of individual information in an information
theoretic sense.
Motivation
In the past, various ad-hoc approaches to anonymizing public records have failed when researchers managed to identify personal information by linking two or more separately innocuous databases. Two well-known instances of successful "Linkage Attacks" have been the Netflix DatabaseNetflix Prize
The Netflix Prize was an open competition for the best collaborative filtering algorithm to predict user ratings for films, based on previous ratings....
and the Massachusetts Group Insurance Commission (GIC) medical encounter
database.
Netflix Prize
NetflixNetflix
Netflix, Inc., is an American provider of on-demand internet streaming media in the United States, Canada, and Latin America and flat rate DVD-by-mail in the United States. The company was established in 1997 and is headquartered in Los Gatos, California...
has offered $1,000,000 prize for a 10% improvement in its recommendation system. Netflix has also released a training dataset for the competing developers to train their systems. While releasing this dataset they had provided a disclaimer: To protect customer privacy, all personal information identifying individual customers has been removed and all customer ids have been replaced by randomly-assigned ids.
Netflix is not the only available movie rating portal on the web; there are many including IMDB. In IMDB also individuals can register and rate movies, moreover they have the option of not keeping their details anonymous. Narayanan and Shmatikov had cleverly linked the Netflix anonymized training database with the Imdb database (using the date of rating by a user) to partly de-anonymize the Netflix training database. Thus clearly the individual information of a user was compromised.
Massachusetts Group Insurance Commission (GIC) medical encounter database
In this case Latanya Sweeney from Carnegie Mellon University linked the anonymized GIC database (which retained the birthdate, sex, and zip code of each patient) and voter registration records to identify the medical record of the governor of Massachusetts.Sensitivity
Getting back on the main stream discussion on Differential Privacy,the sensitivity (
) of a function is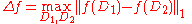for all
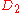, differing in at most one element, and 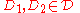.To get more intuition into this let us return to the example of the medical database and a query
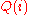(which can also be seen as the function 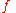) to find how many people in the first 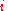rows of the database have diabetes. Clearly, if we change one of the entries in the database then the output of the query 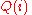will change by at most one. So, the sensitivity of this query is one. It so happens that there are techniques(which we will describe below) using which we can create a differentially private algorithm for functions with low sensitivity.Laplace noise
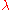Many differentially private algorithms rely on adding controlled noise to functions with low sensitivity. We will elaborate this point by taking a special kind of noise (whose kernel is a Laplace distribution i.e. the probability density function, mean zero and standard deviation ). Now in our case we define the output function of 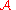as a real valued function (called as the transcript output by 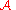) 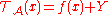, where and 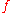is the original real valued query/function we plan to execute on the database. Now clearly 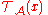can be considered to be a continuous random variable, where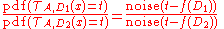which is atmost
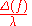. We can consider to be the privacy factor . Thus follows a differentially private mechanism (as can be seen from the definition). If we try to use this concept in our diabetes example then it follows from the above derived fact that in order to have 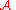as the -differential private algorithm we need to have 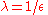.Though we have used Laplacian noise here but we can use other forms of noises which also allows to create a differentially private mechanism, such as the Gaussian Noise (where of course a slight relaxation of the definition of differential privacy is needed).
Composability
If we query an ε-differential privacy mechanism times, the result would be -differentially private.More generally if there is mechanisms
which are 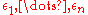differentially private, respectively, then any function of them is 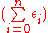-differentially private.Group privacy
In general, ε-differential privacy is designed to protect the privacy between neighboring databases which differ only in one row. This means that no adversary with arbitrary auxiliary information can know if one particular participant submitted his information. However this is also extendable if we want to protect databases differing in rows, which amounts to adversary with arbitrary auxiliary information can know if particular participants submitted their information. This can be achieved because if items change, the probability dilation is bounded by 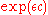instead of 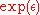, i.e. for D1 and D2 differing on items: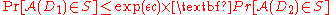Thus setting ε instead to
achieves the desired result (protection of items). In other words, instead of having each item ε-differentially private protected, now every group of items is ε-differentially private protected (and each item is 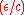-differentially private protected).Proof idea
For three datasets D1, D2, and D3, such that D1 and D2 differ on one item, and D2 and D3 differ on one item (implicitly D1 and D3 differ on at most 2 items), the following holds for an ε-differentially private mechanism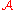: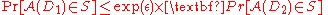,and
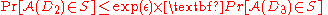
hence:
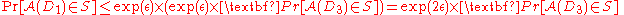
The proof can be extended to
instead of 2.See also
Exponential mechanism (differential privacy)Exponential mechanism (differential privacy)
The exponential mechanism is a technique for designing differentially private algorithms developed by and . Differential privacy is a technique for releasing statistical information about a database without revealing information about its individual entries...
– a technique for designing differentially private algorithms
External links
- Differential Privacy: A Survey of Results by Cynthia Dwork, Microsoft Research April 2008
- Privacy of Dynamic Data: Continual Observation and Pan Privacy by Moni Naor, Institute for Advanced Study November 2009