Dinitz conjecture
Encyclopedia
In combinatorics
, the Dinitz conjecture is a statement about the extension of arrays to partial Latin squares, proposed in 1979 by Jeff Dinitz
, and proved in 1994 by Fred Galvin
.
The Dinitz conjecture, now a theorem, is that given an n × n square array, a set of m symbols with m ≥ n, and for each cell of the array an n-element set drawn from the pool of m symbols, it is possible to choose a way of labeling each cell with one of those elements in such a way that no row or column repeats a symbol.
The Dinitz conjecture is closely related to graph theory
, in which it can be succinctly stated as
for natural 
. It means that the list chromatic index of the complete bipartite graph
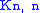equals 
. In fact, Fred Galvin proved the Dinitz conjecture as a special case of his theorem stating that the list chromatic index of any bipartite multigraph is equal to its chromatic index. Moreover, it is also a special case of the edge list coloring conjecture saying that the same holds not only for bipartite graphs, but also for any loopless multigraph.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Dinitz conjecture is a statement about the extension of arrays to partial Latin squares, proposed in 1979 by Jeff Dinitz
Jeff Dinitz
Jeffrey H. Dinitz is an American mathematician, currently teaching combinatorics at the University of Vermont. He is best known for proposing the Dinitz conjecture, which became a major theorem....
, and proved in 1994 by Fred Galvin
Fred Galvin
Frederick William Galvin is a mathematician, currently a professor at the University of Kansas. His research interests include set theory and combinatorics.His notable combinatorial work includes the proof of the Dinitz conjecture...
.
The Dinitz conjecture, now a theorem, is that given an n × n square array, a set of m symbols with m ≥ n, and for each cell of the array an n-element set drawn from the pool of m symbols, it is possible to choose a way of labeling each cell with one of those elements in such a way that no row or column repeats a symbol.
The Dinitz conjecture is closely related to graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, in which it can be succinctly stated as
for natural . It means that the list chromatic index of the complete bipartite graphComplete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
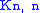equals . In fact, Fred Galvin proved the Dinitz conjecture as a special case of his theorem stating that the list chromatic index of any bipartite multigraph is equal to its chromatic index. Moreover, it is also a special case of the edge list coloring conjecture saying that the same holds not only for bipartite graphs, but also for any loopless multigraph.