Direct limit of groups
Encyclopedia
In mathematics
, a direct limit of groups is the direct limit
of a direct system of groups. These are central objects of study in algebraic topology
, especially stable homotopy theory
and homological algebra
. They are sometimes called stable groups, though this term normally means something quite different in model theory
.
Certain examples of stable groups are easier to study than "unstable" groups, the groups occurring in the limit. This is a priori surprising, given that they are generally infinite-dimensional, constructed as limits of groups with finite-dimensional representations.;
s forms a direct system, via inclusion of matrices in the upper left corner, such as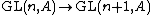
. The stable groups are denoted 
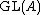or 
.
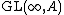Bott periodicity computes the homotopy of the stable unitary group
and stable orthogonal group
.
The Whitehead group
of a ring (the first K-group) can be defined in terms of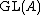
.
Stable homotopy groups of spheres are the stable groups associated with the suspension functor.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a direct limit of groups is the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of a direct system of groups. These are central objects of study in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, especially stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
and homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
. They are sometimes called stable groups, though this term normally means something quite different in model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
.
Certain examples of stable groups are easier to study than "unstable" groups, the groups occurring in the limit. This is a priori surprising, given that they are generally infinite-dimensional, constructed as limits of groups with finite-dimensional representations.;
Examples
Each family of classical groupClassical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s forms a direct system, via inclusion of matrices in the upper left corner, such as
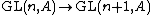. The stable groups are denoted 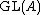or 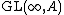.Bott periodicity computes the homotopy of the stable unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
and stable orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
.
The Whitehead group
Whitehead group
Whitehead group in mathematics may mean:* A group W with Ext=0; see Whitehead problem* For a ring, the Whitehead group Wh of a ring A, equal to K_1...
of a ring (the first K-group) can be defined in terms of
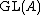.Stable homotopy groups of spheres are the stable groups associated with the suspension functor.