
Dirichlet's approximation theorem
Encyclopedia
In number theory
, Dirichlet's theorem on Diophantine approximation
, also called Dirichlet's approximation theorem, states that for any real number
α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and
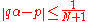
This is a foundational result in diophantine approximation
, showing that any real number has a sequence of good rational approximations: in fact an immediate consequence is that for a given irrational α, the inequality

is satisfied by infinitely many integers p and q. This corollary also shows that the Thue–Siegel–Roth theorem
, a result in the other direction, provides essentially the tightest possible bound, in the sense that the limits on rational approximation of algebraic number
s cannot be improved by lowering the exponent 2 + ε beyond 2.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Dirichlet's theorem on Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, also called Dirichlet's approximation theorem, states that for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and
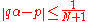
This is a foundational result in diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, showing that any real number has a sequence of good rational approximations: in fact an immediate consequence is that for a given irrational α, the inequality

is satisfied by infinitely many integers p and q. This corollary also shows that the Thue–Siegel–Roth theorem
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
, a result in the other direction, provides essentially the tightest possible bound, in the sense that the limits on rational approximation of algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s cannot be improved by lowering the exponent 2 + ε beyond 2.

