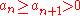Dirichlet's test
Encyclopedia
In mathematics
, Dirichlet's test is a method of testing for the convergence of a series
. It is named after mathematician Johann Dirichlet
who published it in the Journal de Mathématiques Pures et Appliquées
in 1862.
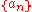is a sequence
of real number
s and
a sequence of complex number
s satisfying
where M is some constant, then the series
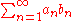
converges.
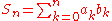and 
.
From summation by parts, we have that
.
Since
is bounded by M and 
, the first of these terms approaches zero, 
as n→∞.
On the other hand, since the sequence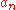
is decreasing, 
is positive for all k, so 
. That is, the magnitude of the partial sum of Bn, times a factor, is less than the upper bound of the partial sum Bn (a value M) times that same factor.
But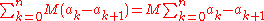
, which is a telescoping series that equals 
and therefore approaches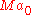 
as n→∞. Thus, 
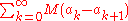converges.
In turn,
by the Direct Comparison test
. The series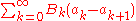
converges, as well, by the Absolute convergence
test. Hence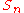
converges.
for the case
Another corollary is that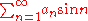
converges whenever
is a decreasing sequence that tends to zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Dirichlet's test is a method of testing for the convergence of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. It is named after mathematician Johann Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
who published it in the Journal de Mathématiques Pures et Appliquées
Journal de Mathématiques Pures et Appliquées
The Journal de Mathématiques Pures et Appliquées is a French monthly scientific journal of mathematics, founded in 1836 by Joseph Liouville. It is published by Elsevier. According to the 2008 Journal Citation Reports, its impact factor is 1.204. Articles are written in English or French.- External...
in 1862.
Statement
The test states that if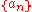 is a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and
a sequence of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s satisfying
-
for every positive integer N
where M is some constant, then the series
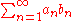
converges.
Proof
Let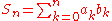 and .From summation by parts, we have that
.Since
is bounded by M and , the first of these terms approaches zero, as n→∞.On the other hand, since the sequence
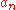is decreasing, is positive for all k, so . That is, the magnitude of the partial sum of Bn, times a factor, is less than the upper bound of the partial sum Bn (a value M) times that same factor.But
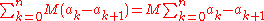, which is a telescoping series that equals and therefore approaches 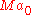as n→∞. Thus, 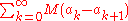converges.In turn,
by the Direct Comparison testComparison test
In mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
. The series
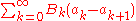converges, as well, by the Absolute convergenceAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
test. Hence
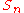converges.Applications
A particular case of Dirichlet's test is the more commonly used alternating series testAlternating series test
The alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.A series of the form...
for the case
-
.
Another corollary is that
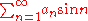
converges whenever
is a decreasing sequence that tends to zero.