Dixmier trace
Encyclopedia
In mathematics, the Dixmier trace, introduced by , is a non-normal trace on a space of linear operators on a Hilbert space
larger than the space of trace class operators.
Some of its applications to noncommutative geometry are described in .
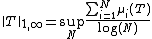
is finite, where the numbers μi(T) are the eigenvalues of |T| arranged in decreasing order. Let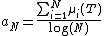
.
The Dixmier trace Trω(T) of T is defined for positive operators T of L1,∞(H) to be
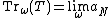
where limω is a scale-invariant positive "extension" of the usual limit, to all bounded sequences. In other words, it has the following properties:
There are many such extensions (such as a Banach limit of α1, α2, α4, α8,...) so there are many different Dixmier traces.
As the Dixmier trace is linear, it extends by linearity to all operators of L1,∞(H).
If the Dixmier trace of an operator is independent of the choice of limω then the operator is called measurable.
A trace φ is called normal if φ(sup xα) = sup φ( xα) for every bounded increasing directed family of positive operators. Any normal trace on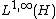
is equal to the usual trace, so the Dixmier trace is an example of a non-normal trace.
If the eigenvalues μi of the positive operator T have the property that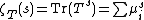
converges for Re(s)>1 and extends to a meromorphic function near s=1 with at most a simple pole at s=1, then the Dixmier trace
of T is the residue at s=1 (and in particular is independent of the choice of ω).
showed that Wodzicki's noncommutative residue
of a pseudodifferential operator on a manifold
is equal to its Dixmier trace.
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
larger than the space of trace class operators.
Some of its applications to noncommutative geometry are described in .
Definition
If H is a Hilbert space, then L1,∞(H) is the space of compact linear operators T on H such that the norm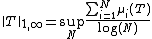is finite, where the numbers μi(T) are the eigenvalues of |T| arranged in decreasing order. Let
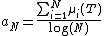.The Dixmier trace Trω(T) of T is defined for positive operators T of L1,∞(H) to be
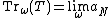
where limω is a scale-invariant positive "extension" of the usual limit, to all bounded sequences. In other words, it has the following properties:
- limω(αn) ≥ 0 if all αn ≥ 0 (positivity)
- limω(αn) = lim(αn) whenever the ordinary limit exists
- limω(α1, α1, α2, α2, α3, ...) = limω(αn) (scale invariance)
There are many such extensions (such as a Banach limit of α1, α2, α4, α8,...) so there are many different Dixmier traces.
As the Dixmier trace is linear, it extends by linearity to all operators of L1,∞(H).
If the Dixmier trace of an operator is independent of the choice of limω then the operator is called measurable.
Properties
- Trω(T) is linear in T.
- If T ≥ 0 then Trω(T) ≥ 0
- If S is bounded then Trω(ST) = Trω(TS)
- Trω(T) does not depend on the choice of inner product on H.
- Trω(T) = 0 for all trace class operators T, but there are compact operators for which it is equal to 1.
A trace φ is called normal if φ(sup xα) = sup φ( xα) for every bounded increasing directed family of positive operators. Any normal trace on
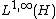is equal to the usual trace, so the Dixmier trace is an example of a non-normal trace.Examples
A compact self-adjoint operator with eigenvalues 1, 1/2, 1/3, ... has Dixmier trace equal to 1.If the eigenvalues μi of the positive operator T have the property that
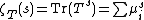
converges for Re(s)>1 and extends to a meromorphic function near s=1 with at most a simple pole at s=1, then the Dixmier trace
of T is the residue at s=1 (and in particular is independent of the choice of ω).
showed that Wodzicki's noncommutative residue
Noncommutative residue
In mathematics, noncommutative residue, defined independently by M. and , is a certain trace on the algebra of pseudodifferential operators on a compact differentiable manifold that is expressed via a local density. In the case of the circle, the noncommutative residue had been studied earlier by...
of a pseudodifferential operator on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is equal to its Dixmier trace.