Double groupoid
Encyclopedia
In mathematics
, especially in higher-dimensional algebra
and homotopy theory, a double groupoid generalises the notion of groupoid
and of category
to a higher dimension.
involving a relationship for both `horizontal' and `vertical' groupoid structures. (A double groupoid can also be considered as a generalization of certain higher-dimensional groups.) The geometry of squares and their composition
s leads to a common representation of a double groupoid in the following diagram
:
where M is a set of `points', H and V are, respectively, `horizontal' and `vertical' groupoids, and S is a set of `squares' with two compositions. The composition laws
for a double groupoid D make it also describable as a groupoid internal to the category of groupoids
.
Given two groupoids H, V over a set M, there is a double groupoid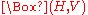
with H,V as horizontal and vertical edge groupoids, and squares given by quadruples
for which we assume always that h, h' are in H, v, v' are in V, and that the initial and final points of these edges match in M as suggested by the notation, that is for example sh = sv, th = sv',..., etc. The compositions are to be inherited from those of H,V, that is:
This construction is the right adjoint to the forgetful functor which takes the double groupoid as above, to the pair of groupoids H,V over M.
Other related constructions are that of a double groupoid with connection and homotopy double groupoids .
whose objects are double groupoids and whose morphisms are double groupoid homomorphisms that are double groupoid diagram (D) functors is called the double groupoid category, or the category of double groupoids.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in higher-dimensional algebra
Higher-dimensional algebra
Supercategories were first introduced in 1970, and were subsequently developed for applications in theoretical physics and mathematical biology or mathematical biophysics....
and homotopy theory, a double groupoid generalises the notion of groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
and of category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
to a higher dimension.
Definition
A double groupoid D is a higher-dimensional groupoidGroupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
involving a relationship for both `horizontal' and `vertical' groupoid structures. (A double groupoid can also be considered as a generalization of certain higher-dimensional groups.) The geometry of squares and their composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
s leads to a common representation of a double groupoid in the following diagram
Diagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
:
where M is a set of `points', H and V are, respectively, `horizontal' and `vertical' groupoids, and S is a set of `squares' with two compositions. The composition laws
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
for a double groupoid D make it also describable as a groupoid internal to the category of groupoids
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
.
Given two groupoids H, V over a set M, there is a double groupoid
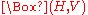with H,V as horizontal and vertical edge groupoids, and squares given by quadruplesfor which we assume always that h, h' are in H, v, v' are in V, and that the initial and final points of these edges match in M as suggested by the notation, that is for example sh = sv, th = sv',..., etc. The compositions are to be inherited from those of H,V, that is:
This construction is the right adjoint to the forgetful functor which takes the double groupoid as above, to the pair of groupoids H,V over M.
Other related constructions are that of a double groupoid with connection and homotopy double groupoids .
Convolution algebra
A convolution C*-algebra of a double groupoid can also be constructed by employing the square diagram D of a double groupoid .Double Groupoid Category
The categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
whose objects are double groupoids and whose morphisms are double groupoid homomorphisms that are double groupoid diagram (D) functors is called the double groupoid category, or the category of double groupoids.