
Double origin topology
Encyclopedia
In mathematics, more specifically general topology
, the double origin topology is an example of a topology
given to the plane R2 with an extra point, say 0*, added. In this case, the double origin topology gives a topology on the set , where ∐ denotes the disjoint union
.
To give the set X a topology means to say which subset
s of X are "open", and to do so in a way that the following axiom
s are met:
s of x are those given by the standard metric topology on We define a countably infinite basis
of neighbourhoods about the point 0 and about the additional point 0*. For the point 0, the basis, index
ed by n, is defined to be: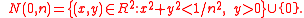
In a similar way, the basis of neighbourhoods of 0* is defined to be: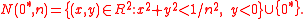
, although it is not completely Hausdorff. In terms of compactness, the space }, along with the double origin topology fails to be either compact, paracompact or locally compact. Finally, it is an example of an arc connected space.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, the double origin topology is an example of a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
given to the plane R2 with an extra point, say 0*, added. In this case, the double origin topology gives a topology on the set , where ∐ denotes the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
.
To give the set X a topology means to say which subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X are "open", and to do so in a way that the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s are met:
- The union of open sets is an open set.
- The finite intersection of open sets is an open set.
- The set X and the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ are open sets.
Construction
Given a point x belonging to X, such that and , the neighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
s of x are those given by the standard metric topology on We define a countably infinite basis
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
of neighbourhoods about the point 0 and about the additional point 0*. For the point 0, the basis, index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
ed by n, is defined to be:
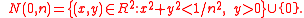
In a similar way, the basis of neighbourhoods of 0* is defined to be:
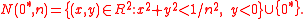
Properties
The space }, along with the double origin topology is an example of a Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, although it is not completely Hausdorff. In terms of compactness, the space }, along with the double origin topology fails to be either compact, paracompact or locally compact. Finally, it is an example of an arc connected space.

