
Doubling measure
Encyclopedia
In mathematics
, a metric space
X with metric d is said to be doubling if there is some constant M > 0 such that for any x in X and r > 0, the ball B(x, r) = {y:|x − y| < r} may be contained in a union of no more than M many balls with radius r/2. Euclidean spaces ℝd equipped with the usual Euclidean metric are examples of doubling spaces where the doubling constant M depends on the dimension d.
function. This means that one can essentially think of the metric space as a subset of Euclidean space. Not all metric spaces may be embedded in Euclidean space. Doubling metric spaces, on the other hand, would seem like they have more of a chance, since the doubling condition says, in a way, that the metric space is not finite dimensional. However, this is still not the case in general. The Heisenberg group with its Carnot metric is an example of a doubling metric space which cannot be embedded in any Euclidean space.
Assouad's Theorem states that, for a M-doubling metric space X, if we give it the metric d(x, y)ε for some 0 < ε < 1, then there is a L-bi-Lipschitz map f:X → ℝd, where d and L depend on M and ε.
on a metric space X is said to be doubling if the measure of any ball is approximately the measure of its double, or more precisely, if there is a constant C > 0 such that
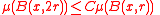
for all x in X and r > 0. In this case, we say μ is C-doubling.
A measure space that supports a doubling measure is necessarily a doubling metric space, where the doubling constant depends on the constant C.
Conversely, any compact
doubling metric space supports a doubling measure.
on a Euclidean space. One can, however, have doubling measures on Euclidean space that are singular with respect to Lebesgue measure. One example on the real line is the weak limit of the following sequence of measures:

One can construct another singular doubling measure μ on the interval [0, 1] as follows: for each k ≥ 0, partition the unit interval [0,1] into 3k intervals of length 3−k. Let Δ be the collection of all such intervals in [0,1] obtained for each k (these are the triadic intervals), and for each such interval I, let m(I) denote its "middle third" interval. Fix 0 < δ < 1 and let μ be the measure such that μ([0, 1]) = 1 and for each triadic interval I, μ(m(I)) = δμ(I). Then this gives a singular measure on [0, 1] singular to Lebesgue measure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X with metric d is said to be doubling if there is some constant M > 0 such that for any x in X and r > 0, the ball B(x, r) = {y:|x − y| < r} may be contained in a union of no more than M many balls with radius r/2. Euclidean spaces ℝd equipped with the usual Euclidean metric are examples of doubling spaces where the doubling constant M depends on the dimension d.
Assouad's embedding theorem
An important question in metric space geometry is to characterize those metric spaces that can be embedded in some Euclidean space by a bi-LipschitzLipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
function. This means that one can essentially think of the metric space as a subset of Euclidean space. Not all metric spaces may be embedded in Euclidean space. Doubling metric spaces, on the other hand, would seem like they have more of a chance, since the doubling condition says, in a way, that the metric space is not finite dimensional. However, this is still not the case in general. The Heisenberg group with its Carnot metric is an example of a doubling metric space which cannot be embedded in any Euclidean space.
Assouad's Theorem states that, for a M-doubling metric space X, if we give it the metric d(x, y)ε for some 0 < ε < 1, then there is a L-bi-Lipschitz map f:X → ℝd, where d and L depend on M and ε.
Definition
A measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a metric space X is said to be doubling if the measure of any ball is approximately the measure of its double, or more precisely, if there is a constant C > 0 such that
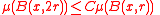
for all x in X and r > 0. In this case, we say μ is C-doubling.
A measure space that supports a doubling measure is necessarily a doubling metric space, where the doubling constant depends on the constant C.
Conversely, any compact
Compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
doubling metric space supports a doubling measure.
Examples
A simple example of a doubling measure is Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on a Euclidean space. One can, however, have doubling measures on Euclidean space that are singular with respect to Lebesgue measure. One example on the real line is the weak limit of the following sequence of measures:

One can construct another singular doubling measure μ on the interval [0, 1] as follows: for each k ≥ 0, partition the unit interval [0,1] into 3k intervals of length 3−k. Let Δ be the collection of all such intervals in [0,1] obtained for each k (these are the triadic intervals), and for each such interval I, let m(I) denote its "middle third" interval. Fix 0 < δ < 1 and let μ be the measure such that μ([0, 1]) = 1 and for each triadic interval I, μ(m(I)) = δμ(I). Then this gives a singular measure on [0, 1] singular to Lebesgue measure.

