Dual impedance
Encyclopedia
Dual impedance
and dual network are terms used in electronic network analysis. The dual of an impedance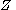
is its algebraic inverse 
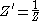. Note that 
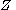and 
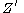are the duals of each other, that is, they are reciprocal. For this reason the dual impedance is also called the inverse impedance. The dual of a network of impedances is that network whose impedance is 
. In the case of a network with more than one port
the impedance looking into each of the ports must simultaneously be dual.
Another way of stating this is that the dual of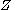
is the admittance 
.
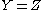This is consistent with the definition of dual as being that circuit whose voltages and currents are interchanged since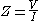
and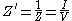 
. To do this, Z and Z' are scaled to the nominal impedance Z0 so that;
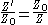
Z0 is usually taken to be a purely real number R0, so Z' is only changed by a real factor of R02. In other words, the dual remains qualitatively the same circuit but all the component values must be scaled quantitively by R02.
.
This completes the drawing of Z'. This method also serves to demonstrate that the dual of a mesh transforms in to a node and the dual of a node transforms in to a mesh. Two useful examples are given below, both to illustrate the process and to give some further examples of dual networks.
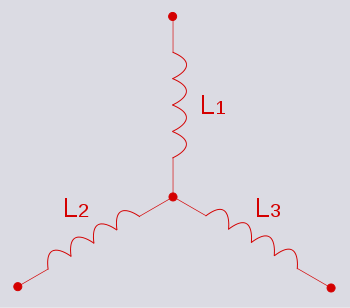
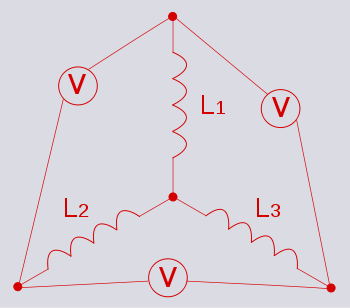
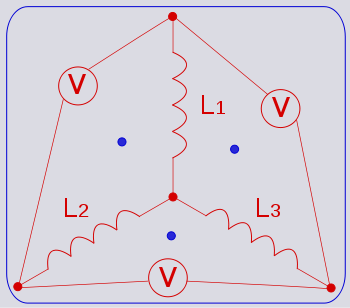
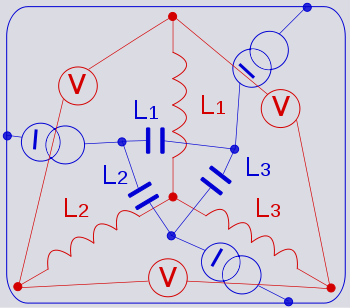
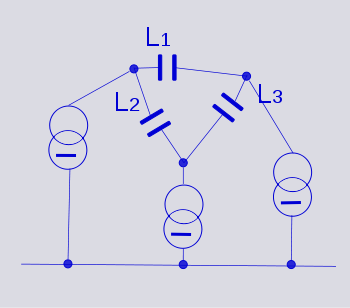
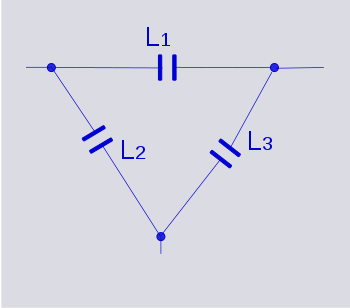
It is now clear that the dual of a star network of inductors is a delta network of capacitor
s. This dual circuit is not the same thing as a star-delta (Y-Δ) transformation. A Y-Δ transform results in an equivalent circuit
, not a dual circuit.
It can now be seen that the dual of a Cauer low-pass filter is still a Cauer low-pass filter. It does not transform into a high-pass filter as might have been expected. Note, however, that the first element is now a shunt component instead of a series component.
Electrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
and dual network are terms used in electronic network analysis. The dual of an impedance
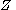is its algebraic inverse 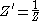. Note that 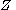and 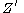are the duals of each other, that is, they are reciprocal. For this reason the dual impedance is also called the inverse impedance. The dual of a network of impedances is that network whose impedance is . In the case of a network with more than one portTwo-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
the impedance looking into each of the ports must simultaneously be dual.
Another way of stating this is that the dual of
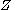is the admittance 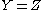.This is consistent with the definition of dual as being that circuit whose voltages and currents are interchanged since
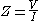and 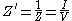Scaled and normalised duals
In a real design situation it is usually desired to find the dual of an impedance with respect to some nominal or characteristic impedanceCharacteristic impedance
The characteristic impedance or surge impedance of a uniform transmission line, usually written Z_0, is the ratio of the amplitudes of a single pair of voltage and current waves propagating along the line in the absence of reflections. The SI unit of characteristic impedance is the ohm...
. To do this, Z and Z' are scaled to the nominal impedance Z0 so that;
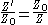
Z0 is usually taken to be a purely real number R0, so Z' is only changed by a real factor of R02. In other words, the dual remains qualitatively the same circuit but all the component values must be scaled quantitively by R02.
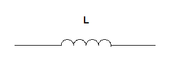
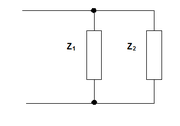
Duals of basic circuit elements
| Element | Z | Dual | Z' |
|---|---|---|---|
 |
 |
 |
 |
| |
 |
|
 |
 |
 |
 |
 |
| |
 |
|
 |
 |
 |
 |
 |
| |
 |
|
 |
 |
 |
||
| |
|
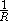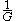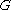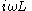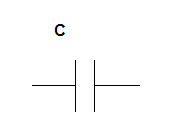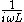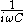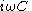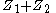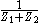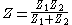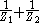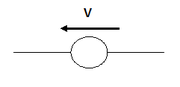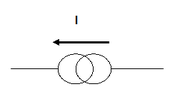Graphical Method
There is a graphical method of obtaining the dual of a network which is often easier to use than the mathematical expression for the impedance. Starting with a circuit diagram of the network in question, Z, the following steps are drawn on the diagram to produce Z' superimposed on top of Z. Typically, Z' will be drawn in a different colour to help distinguish it from the original, or, if using CAD, Z' can be drawn on a different layerLayer
Layer may refer to:* A layer of archaeological deposits in an excavation* A layer hen, a hen raised to produce eggs* Stratum, a layer of rock or soil with internally consistent characteristics...
.
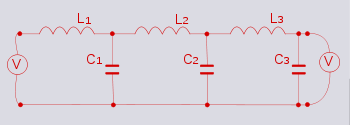
- A generator is connected to each portTwo-port networkA two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
of the original network. The purpose of this step is to prevent the ports from being "lost" in the inversion process. This happens because a port left open circuit will transform into a short circuit and disappear. - A dot is drawn at the centre of each meshMesh analysisMesh analysis is a method that is used to solve planar circuits for the currents at any place in the circuit. Planar circuits are circuits that can be drawn on a plane surface with no wires crossing each other. A more general technique, called loop analysis can be applied to any circuit, planar...
of the network Z. These dots will become the circuit nodesNode (circuits)In electrical engineering, node refers to any point on a circuit where two or more circuit elements meet. For two nodes to be different, their voltages must be different. Without any further knowledge, it is easy to establish how to find a node by using Ohm's Law: V=IR. When looking at circuit...
of Z'. - A conductor is drawn which entirely encloses the network Z. This conductor also becomes a node of Z'.
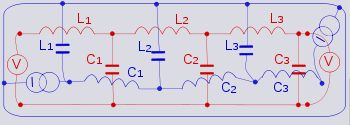
- For each circuit element of Z, its dual is drawn between the nodes in the centre of the meshes either side of Z. Where Z is on the edge of the network, one of these nodes will be the enclosing conductor from the previous step.
This completes the drawing of Z'. This method also serves to demonstrate that the dual of a mesh transforms in to a node and the dual of a node transforms in to a mesh. Two useful examples are given below, both to illustrate the process and to give some further examples of dual networks.
Example - star network
It is now clear that the dual of a star network of inductors is a delta network of capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
s. This dual circuit is not the same thing as a star-delta (Y-Δ) transformation. A Y-Δ transform results in an equivalent circuit
Equivalent circuit
In electrical engineering and science, an equivalent circuit refers to a theoretical circuit that retains all of the electrical characteristics of a given circuit. Often, an equivalent circuit is sought that is the simplest form of a more complex circuit in order to aid analysis. In its most common...
, not a dual circuit.
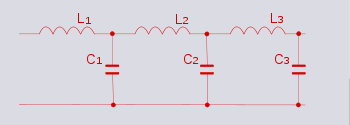
Example - Cauer network
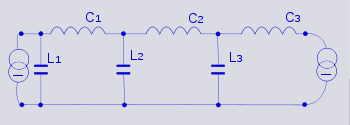
Filters designed using Cauer's topology of the first form are low-pass filters consisting of a ladder network of series inductors and shunt capacitors.It can now be seen that the dual of a Cauer low-pass filter is still a Cauer low-pass filter. It does not transform into a high-pass filter as might have been expected. Note, however, that the first element is now a shunt component instead of a series component.