Dual of BCH is an independent source
Encyclopedia
A certain family of BCH code
s have a particularly useful property, which is that
treated as linear operators, their dual operators turns their input into an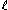
-wise independent source
. That is, the set of vectors from the input vector space
are mapped to an
-wise independent source. The proof of this fact below as the following Lemma and Corollary is useful in derandomizing the algorithm for a 
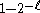-approximation to MAXEkSAT
.
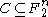be a linear code such that 
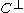has distance greater than 
. Then 
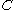is an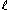 
-wise independent source.
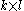matrix M, where k is greater than or equal to l, such that the rank of M is l, for all 
, 
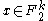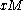takes every value in 
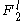the same number of times.
Since M has rank l, we can write M as two matrices of the same size,
and 
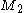, where 
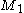has rank equal to l. This means that 
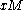can be rewritten as 
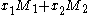for some 
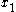and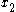 
.
If we consider M written with respect to a basis where the first l rows are the identity matrix, then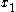
has zeros wherever 
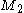has nonzero rows, and 
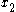has zeros wherever 
has nonzero rows.
Now any value y, where
, can be written as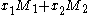 
for some vectors 
.
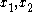We can rewrite this as:
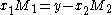
Fixing the value of the last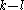
coordinates of
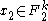(note that there are exactly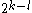 
such choices), we can rewrite this equation again as:
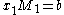for some b.
Since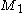
has rank equal to l, there
is exactly one solution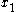
, so the total number of solutions is exactly 
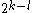, proving the lemma.
linear code.
Let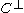
be BCH2,log n,ℓ+1. Then 
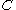is an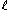 
-wise independent source of size 
.
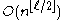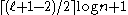. So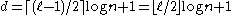 
.
So the cardinality of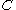
considered as a set is just
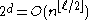, proving the Corollary.
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s have a particularly useful property, which is that
treated as linear operators, their dual operators turns their input into an
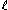-wise independent sourcePairwise independence
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent...
. That is, the set of vectors from the input vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
are mapped to an
-wise independent source. The proof of this fact below as the following Lemma and Corollary is useful in derandomizing the algorithm for a 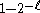-approximation to MAXEkSATMAXEkSAT
MAXEkSAT is a problem in computational complexity theory that is a maximization version of the Boolean satisfiability problem 3SAT.In MAXEkSAT, each clause has exactly k literals, with k ≥ 3, and is in conjunctive normal form...
.
Lemma
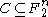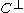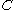Let be a linear code such that has distance greater than . Then is an 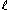-wise independent source.Proof of Lemma
It is sufficient to show that given any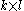 matrix M, where k is greater than or equal to l, such that the rank of M is l, for all 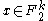, 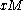takes every value in 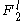the same number of times.Since M has rank l, we can write M as two matrices of the same size,
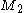and , where 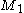has rank equal to l. This means that 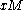can be rewritten as 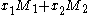for some 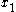and 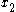.If we consider M written with respect to a basis where the first l rows are the identity matrix, then
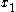has zeros wherever 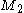has nonzero rows, and 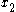has zeros wherever has nonzero rows.Now any value y, where
, can be written as 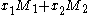for some vectors 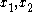.We can rewrite this as:
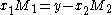
Fixing the value of the last
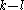coordinates of 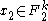(note that there are exactly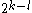 such choices), we can rewrite this equation again as:
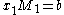for some b.Since
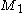has rank equal to l, thereis exactly one solution
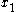, so the total number of solutions is exactly 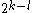, proving the lemma.Corollary
Recall that BCH2,m,d is an linear code.Let
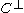be BCH2,log n,ℓ+1. The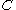n is an 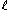-wise independent source of size 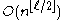.Proof of Corollary
The dimension d of C is just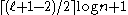. So 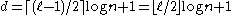.So the cardinality of
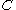considered as a set is just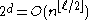, proving the Corollary.