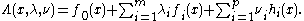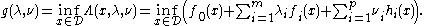Dual problem
Encyclopedia
In constrained optimization
, it is often possible to convert the primal problem (i.e. the original form of the optimization problem) to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem
. The Lagrangian dual problem is obtained by forming the Lagrangian
, using nonnegative Lagrangian multipliers to add the constraints to the objective function, and then solving for some primal variable values that minimize the Lagrangian. This solution gives the primal variables as functions of the Lagrange multipliers, which are called dual variables, so that the new problem is to maximize the objective function with respect to the dual variables under the derived constraints on the dual variables (including at least the nonnegativity).
The solution of the dual problem provides an upper bound to the solution of the primal problem. However in general the optimal values of the primal and dual problems need not be equal. Their difference is called the duality gap
. For convex optimization problems, the duality gap is zero under a constraint qualification condition. Thus, a solution to the dual problem provides a bound on the value of the solution to the primal problem; when the problem is convex and satisfies a constraint qualification, then the value of an optimal solution of the primal problem is given by the dual problem.
In general given two dual pair
s separated locally convex spaces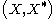 and
and 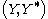 . Then given the function
. Then given the function 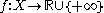 , we can define the primal problem by
, we can define the primal problem by
If there are constraint conditions, these can be built in to the function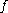 by letting
by letting 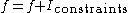 where
where  is the indicator function
is the indicator function
. Then let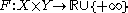 be a perturbation function
be a perturbation function
such that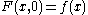 .
.
The duality gap
is the difference of the right and left hand side of the inequality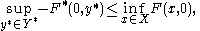
where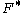 is the convex conjugate
is the convex conjugate
in both variables.
problems are optimization
problems in which the objective function and the constraints
are all linear
. In the primal problem, the objective function is a linear combination of n variables. There are m constraints, each of which places an upper bound on a linear combination of the n variables. The goal is to maximize the value of the objective function subject to the constraints. A "solution" is a vector (a list) of n values that achieves the maximum value for the objective function.
In the dual problem, the objective function is a linear combination of the m values that are the limits in the m constraints from the primal problem. There are n "dual constraints", each of which places a lower bound on a linear combination of m "dual variables".
of directions to move that increases the objective function. Moving in any such direction is said to remove "slack" between the candidate solution and one or more constraints. An "infeasible" value of the candidate solution is one that exceeds one or more of the constraints.
In the dual problem, the dual vector multiplies the constants that determine the positions of the constraints in the primal. Varying the dual vector in the dual problem is equivalent to revising the upper bounds in the primal problem. The lowest upper bound is sought. That is, the dual vector is minimized in order to remove slack between the candidate positions of the constraints and the actual optimum. An infeasible value of the dual vector is one that is too low. It sets the candidate positions of one or more of the constraints in a position that excludes the actual optimum.
This intuition is made formal by the equations in Linear programming: Duality.
To ensure that the global maximum of a non-linear problem can be identified easily, the problem formulation often requires that the functions be convex and have compact lower level sets.
This is the significance of the Karush–Kuhn–Tucker conditions. They provide necessary conditions for identifying local optima of non-linear programming problems. There are additional conditions (constraint qualifications) that are necessary so that it will be possible to define the direction to an optimal solution. An optimal solution is one that is a local optimum, but possibly not a global optimum.
problem in standard form

with the domain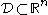 having non-empty interior, the Lagrangian function
having non-empty interior, the Lagrangian function  is defined as
is defined as
The vectors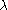 and
and  are called the dual variables or Lagrange multiplier vectors associated with the problem. The Lagrange dual function
are called the dual variables or Lagrange multiplier vectors associated with the problem. The Lagrange dual function 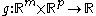 is defined as
is defined as
The dual function g is concave, even when the initial problem is not convex. The dual function yields lower bounds on the optimal value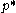 of the initial problem; for any
of the initial problem; for any 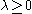 and any
and any  we have
we have 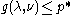 .
.
If a constraint qualification such as Slater's condition
holds and the original problem is convex, then we have strong duality, i.e.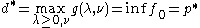 .
.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, it is often possible to convert the primal problem (i.e. the original form of the optimization problem) to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem
Fenchel's duality theorem
In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel.Let ƒ be a proper convex function on Rn and let g be a proper concave function on Rn...
. The Lagrangian dual problem is obtained by forming the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
, using nonnegative Lagrangian multipliers to add the constraints to the objective function, and then solving for some primal variable values that minimize the Lagrangian. This solution gives the primal variables as functions of the Lagrange multipliers, which are called dual variables, so that the new problem is to maximize the objective function with respect to the dual variables under the derived constraints on the dual variables (including at least the nonnegativity).
The solution of the dual problem provides an upper bound to the solution of the primal problem. However in general the optimal values of the primal and dual problems need not be equal. Their difference is called the duality gap
Duality gap
In optimization problems in applied mathematics, the duality gap is the difference between the primal and dual solutions. If d^* is the optimal dual value and p^* is the optimal primal value then the duality gap is equal to p^* - d^*. This value is always greater than or equal to 0. The duality...
. For convex optimization problems, the duality gap is zero under a constraint qualification condition. Thus, a solution to the dual problem provides a bound on the value of the solution to the primal problem; when the problem is convex and satisfies a constraint qualification, then the value of an optimal solution of the primal problem is given by the dual problem.
Duality principle
In optimization theory, the duality principle states that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem.In general given two dual pair
Dual pair
In functional analysis and related areas of mathematics a dual pair or dual system is a pair of vector spaces with an associated bilinear form....
s separated locally convex spaces
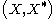 and
and 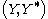 . Then given the function
. Then given the function 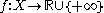 , we can define the primal problem by
, we can define the primal problem by
If there are constraint conditions, these can be built in to the function
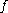 by letting
by letting 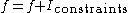 where
where  is the indicator function
is the indicator functionCharacteristic function (convex analysis)
In the field of mathematics known as convex analysis, the characteristic function of a set is a convex function that indicates the membership of a given element in that set...
. Then let
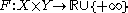 be a perturbation function
be a perturbation functionPerturbation function
In mathematical optimization, the perturbation function is any function which relates to primal and dual problems. The name comes from the fact that any such function defines a perturbation of the initial problem...
such that
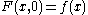 .
.The duality gap
Duality gap
In optimization problems in applied mathematics, the duality gap is the difference between the primal and dual solutions. If d^* is the optimal dual value and p^* is the optimal primal value then the duality gap is equal to p^* - d^*. This value is always greater than or equal to 0. The duality...
is the difference of the right and left hand side of the inequality
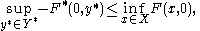
where
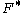 is the convex conjugate
is the convex conjugateConvex conjugate
In mathematics, convex conjugation is a generalization of the Legendre transformation. It is also known as Legendre–Fenchel transformation or Fenchel transformation .- Definition :...
in both variables.
The linear case
Linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problems are optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problems in which the objective function and the constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
are all linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
. In the primal problem, the objective function is a linear combination of n variables. There are m constraints, each of which places an upper bound on a linear combination of the n variables. The goal is to maximize the value of the objective function subject to the constraints. A "solution" is a vector (a list) of n values that achieves the maximum value for the objective function.
In the dual problem, the objective function is a linear combination of the m values that are the limits in the m constraints from the primal problem. There are n "dual constraints", each of which places a lower bound on a linear combination of m "dual variables".
Relationship between the primal problem and the dual problem
In the linear case, in the primal problem, from each sub-optimal point that satisfies all the constraints, there is a direction or subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of directions to move that increases the objective function. Moving in any such direction is said to remove "slack" between the candidate solution and one or more constraints. An "infeasible" value of the candidate solution is one that exceeds one or more of the constraints.
In the dual problem, the dual vector multiplies the constants that determine the positions of the constraints in the primal. Varying the dual vector in the dual problem is equivalent to revising the upper bounds in the primal problem. The lowest upper bound is sought. That is, the dual vector is minimized in order to remove slack between the candidate positions of the constraints and the actual optimum. An infeasible value of the dual vector is one that is too low. It sets the candidate positions of one or more of the constraints in a position that excludes the actual optimum.
This intuition is made formal by the equations in Linear programming: Duality.
Economic interpretation
If we interpret our primal LP problem as a classical "Resource Allocation" problem, its dual can be interpreted as a "Resource Valuation" problem.The non-linear case
In non-linear programming, the constraints are not necessarily linear. Nonetheless, many of the same principles apply.To ensure that the global maximum of a non-linear problem can be identified easily, the problem formulation often requires that the functions be convex and have compact lower level sets.
This is the significance of the Karush–Kuhn–Tucker conditions. They provide necessary conditions for identifying local optima of non-linear programming problems. There are additional conditions (constraint qualifications) that are necessary so that it will be possible to define the direction to an optimal solution. An optimal solution is one that is a local optimum, but possibly not a global optimum.
The strong Lagrangian principle: Lagrange duality
Given a nonlinear programmingNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
problem in standard form

with the domain
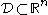 having non-empty interior, the Lagrangian function
having non-empty interior, the Lagrangian function  is defined as
is defined asThe vectors
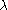 and
and  are called the dual variables or Lagrange multiplier vectors associated with the problem. The Lagrange dual function
are called the dual variables or Lagrange multiplier vectors associated with the problem. The Lagrange dual function 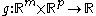 is defined as
is defined asThe dual function g is concave, even when the initial problem is not convex. The dual function yields lower bounds on the optimal value
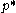 of the initial problem; for any
of the initial problem; for any 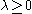 and any
and any  we have
we have 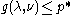 .
.If a constraint qualification such as Slater's condition
Slater's condition
In mathematics, Slater's condition is a sufficient condition for strong duality to hold for a convex optimization problem. This is a specific example of a constraint qualification...
holds and the original problem is convex, then we have strong duality, i.e.
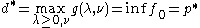 .
.Convex problems
For a convex minimization problem with inequality constraints,-
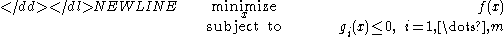
the Lagrangian dual problem is-
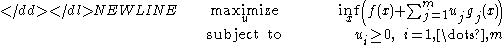
where the expression within parentheses is the Langrange dual function. Provided that the functions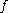 and
and  are continuously differentiable, the infimum occurs where the gradient is equal to zero. The problem
are continuously differentiable, the infimum occurs where the gradient is equal to zero. The problem
-

is called the Wolfe dual problem. This problem may be difficult to deal with computationally, because the objective function is not concave in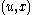 and the equality constraint
and the equality constraint 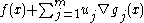 is nonlinear in general, so the Wolfe dual problem is typically a nonconvex optimization problem and weak duality holds.
is nonlinear in general, so the Wolfe dual problem is typically a nonconvex optimization problem and weak duality holds.
History
According to George DantzigGeorge DantzigGeorge Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....
, the duality theorem for linear optimization was conjectured by John von NeumannJohn von NeumannJohn von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, immediately after Dantzig presented the linear programming problem. Von Neumann noted that he was using information from his game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, and conjectured that two person zero sum matrix game was equivalent to linear programming. Rigorous proofs were first published in 1948 by Albert W. TuckerAlbert W. TuckerAlbert William Tucker was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming....
and his group. (Dantzig's forward to Nering and Tucker, 1993)
Books
- Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.
- William J. Cook, William H. Cunningham, William R. Pulleyblank, Alexander Schrijver; Combinatorial Optimization; John Wiley & Sons; 1 edition (November 12, 1997); ISBN 0-471-55894-X.
- Dantzig, G.B., 1963. Linear Programming and Extensions, Princeton University Press, Princeton, NJ.| |unused_data=authorlink2=Claude Lemaréchal}}| |unused_data=authorlink2=Claude Lemaréchal}}. ) |}}
- Nering, E.D and Tucker, A.W., 1993, Linear Programming and Related Problems, Academic Press, Boston, MA.
- Christos H. Papadimitriou and Kenneth SteiglitzKenneth SteiglitzDr. Kenneth "Ken" Steiglitz is a professor of computer science at Princeton University. He was born in Weehawken, New Jersey on January 30, 1939. He received his Doctor of Engineering Science from New York University in 1963. In 1997 he was inducted as a Fellow of the Association for Computing...
Combinatorial Optimization : Algorithms and Complexity; Dover Pubns; (paperback, Unabridged edition, July 1998) ISBN 0-486-40258-4.
-
-