Duhamel's integral
Encyclopedia
In theory of vibration
s, Duhamel's integral is a way of calculating the response of linear system
s and structures to arbitrary time-varying external excitation
s.
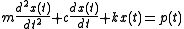
where m is the (equivalent) mass, x stands for the amplitude of vibration, t for time, c for the viscous damping coefficient, and k for the stiffness
of the system or structure.
If a system is initially rest at its equilibrium
position, from where it is acted upon by a unit-impulse at the instance t=0, i.e., p(t) in the equation above is a delta function δ(t),
, then by solving the differential equation one can get a fundamental solution
(known as a unit-impulse response function)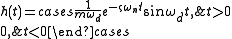
where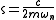
is called the damping ratio
of the system,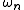
is the natural angular frequency
of the undamped system (when c=0) and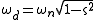
is the circular frequency when damping effect is taken into account (when 
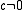). If the impulse happens at t=τ instead of t=0, i.e. 
, the impulse response is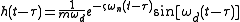
，
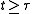
of a series of impulses: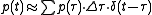
then it is known from the linearity of system that the overall response can also be broken down into the superposition of a series of impulse-responses: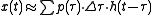
Letting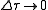
, and replacing the summation by integration
, the above equation is strictly valid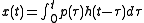
Substituting the expression of h(t-τ) into the above equation leads to the general expression of Duhamel's integral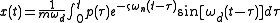
:
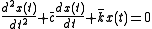, where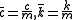 
The solution of this equation is: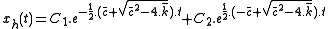
The substitution: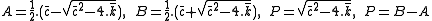
leads to: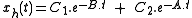
One partial solution of the non-homogeneous equation: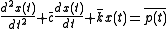
, where 
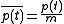, could be obtained by the Lagrangian method for deriving partial solution of non-homogeneous ordinary differential equations.
This solution has the form: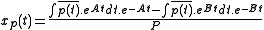
Now substituting: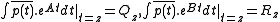
,where 
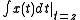is the primitive
of x(t) computed at t=z, in the case z=t this integral is the primitive itself, yields:
Finally the general solution of the above non-homogeneous equation is represented as: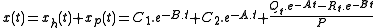
with time derivative: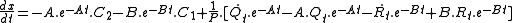
, where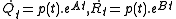 
In order to find the unknown constants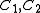
, zero initial conditions will be applied:
⇒ 
⇒ 
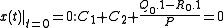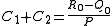
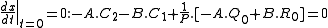Now combining both initial conditions together, the next system of equations is observed:
The back substitution of the constants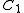
and 
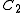into the above expression for x(t) yields: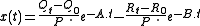
Replacing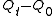
and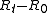 
(the difference between the primitives at t=t and t=0) with definite integrals
(by another variable τ) will reveal the general solution with zero initial conditions, namely: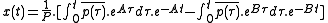
Finally substituting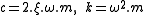
, accordingly 
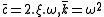, where ξ<1 yields:
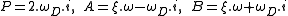, where 
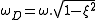and i is the imaginary unit
.
Substituting this expressions into the above general solution with zero initial conditions and using the Euler's exponential formula
will lead to canceling out the imaginary terms and reveals the Duhamel's solution: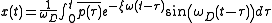
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s, Duhamel's integral is a way of calculating the response of linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s and structures to arbitrary time-varying external excitation
Excitation
-Science:* The excited state of an atom* The excitatory postsynaptic potential* The excitation provided with an electrical generator or alternator-Agitation:*Excitement...
s.
Background
The response of a linear, viscously damped single-degree of freedom (SDOF) system to a time-varying mechanical excitation p(t) is given by the following second-order ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
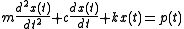
where m is the (equivalent) mass, x stands for the amplitude of vibration, t for time, c for the viscous damping coefficient, and k for the stiffness
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
of the system or structure.
If a system is initially rest at its equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
position, from where it is acted upon by a unit-impulse at the instance t=0, i.e., p(t) in the equation above is a delta function δ(t),
, then by solving the differential equation one can get a fundamental solutionFundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
(known as a unit-impulse response function)
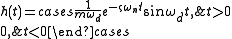
where
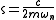is called the damping ratioDamping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
of the system,
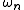is the natural angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the undamped system (when c=0) and
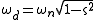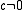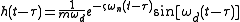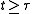
is the circular frequency when damping effect is taken into account (when ). If the impulse happens at t=τ instead of t=0, i.e. , the impulse response is，Conclusion
Regarding the arbitrarily varying excitation p(t) as a superpositionSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of a series of impulses:
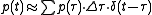
then it is known from the linearity of system that the overall response can also be broken down into the superposition of a series of impulse-responses:
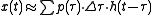
Letting
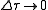, and replacing the summation by integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, the above equation is strictly valid
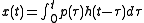
Substituting the expression of h(t-τ) into the above equation leads to the general expression of Duhamel's integral
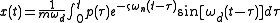
Mathematical Proof
The above SDOF dynamic equilibrium equation in the case p(t)=0 is the homogeneous equationHomogeneous differential equation
The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...
:
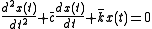, where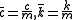 The solution of this equation is:
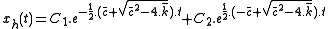
The substitution:
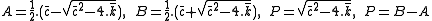leads to: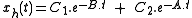One partial solution of the non-homogeneous equation:
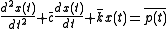, where 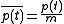, could be obtained by the Lagrangian method for deriving partial solution of non-homogeneous ordinary differential equations.This solution has the form:
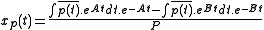
Now substituting:
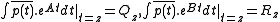,where 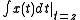is the primitiveAntiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of x(t) computed at t=z, in the case z=t this integral is the primitive itself, yields:
Finally the general solution of the above non-homogeneous equation is represented as:
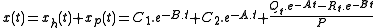
with time derivative:
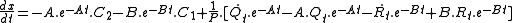, where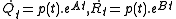 In order to find the unknown constants
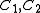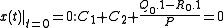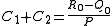
, zero initial conditions will be applied: ⇒ ⇒ 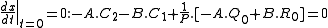Now combining both initial conditions together, the next system of equations is observed:
The back substitution of the constants
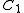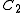and into the above expression for x(t) yields: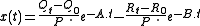Replacing
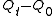and 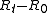(the difference between the primitives at t=t and t=0) with definite integralsIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
(by another variable τ) will reveal the general solution with zero initial conditions, namely:
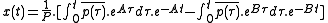
Finally substituting
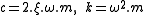, accordingly 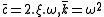, where ξ<1 yields: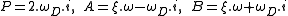, where 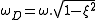and i is the imaginary unitImaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
Substituting this expressions into the above general solution with zero initial conditions and using the Euler's exponential formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
will lead to canceling out the imaginary terms and reveals the Duhamel's solution:
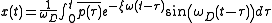
External links
- Duhamel's formula at "Dispersive Wiki".