Damping ratio - AbsoluteAstronomy.com

Engineering

Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...

, the damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system is "trying" to return to its equilibrium position, but overshoots it. Sometimes losses (eg friction

Friction

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...

al) damp

Damping

In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...

the system and can cause the oscillations to gradually decay in amplitude towards zero. The damping ratio is a measure of describing how rapidly the oscillations decay from one bounce to the next.

The behaviour of oscillating systems is often of interest in a diverse range of disciplines that include control engineering

Control engineering

Control engineering or Control systems engineering is the engineering discipline that applies control theory to design systems with predictable behaviors...

, mechanical engineering

Mechanical engineering

Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...

, structural engineering

Structural engineering

Structural engineering is a field of engineering dealing with the analysis and design of structures that support or resist loads. Structural engineering is usually considered a specialty within civil engineering, but it can also be studied in its own right....

and electrical engineering

Electrical engineering

Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...

. The physical quantity that is oscillating varies greatly, and could be the swaying of a tall building in the wind, or the speed of an electric motor

Electric motor

An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...

, but a normalised, or non-dimensionalised approach can be convenient in describing common aspects of behavior.

Oscillation modes

Were the spring–mass system completely lossless, the mass would oscillate indefinitely, each bounce of equal height to the last. This hypothetical case is called undamped.
If the system contained high losses, for example if the spring–mass experiment were conducted in a viscous fluid, the mass could slowly return to its rest position without ever overshooting. This case is called overdamped.
Commonly, the mass tends to overshoot its starting position, and then return, overshooting again. With each overshoot, some energy in the system is dissipated, and the oscillations die towards zero. This case is called underdamped.
Between the overdamped and underdamped cases, there exists a certain level of damping at which the system will just fail to overshoot and will not make a single oscillation. The key difference between critical damping and overdamping is that, in critical damping, the system returns to equilibrium in the minimum amount of time. This case is called critical damping.

Definition

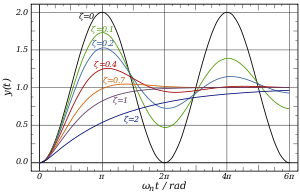
The damping ratio is a parameter, usually denoted by ζ (zeta), that characterizes the frequency response

Frequency response

Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...

of a second order ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

. It is particularly important in the study of control theory

Control theory

Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...

. It is also important in the harmonic oscillator

Harmonic oscillator

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....

.

The damping ratio provides a mathematical means of expressing the level of damping in a system relative to critical damping. For a damped harmonic oscillator with mass m, damping coefficient c, and spring constant k, it can be defined as the ratio of the damping coefficient in the system's differential equation to the critical damping coefficient:

where the system differential equation is

and the corresponding critical damping coefficient is

The damping ratio is dimensionless, being the ratio of two coefficients of identical units.

The damping ratio is also related to the logarithmic decrement

Logarithmic decrement

Logarithmic decrement, δ, is used to find the damping ratio of an underdamped system in the time domain. The logarithmic decrement is the natural log of the ratio of the amplitudes of any two successive peaks:...

for underdamped vibrations via the relation

This relation is only meaningful for underdamped systems because the logarithmic decrement is defined as the natural log of the ratio of any two successive amplitudes, and only underdamped systems exhibit oscillation.

Derivation

Using the natural frequency of the simple harmonic oscillator

and the definition of the damping ratio above, we can rewrite this as:

This equation can be solved with the ansatz

Ansatz

Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...

where C and s are both complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

constants. That ansatz assumes a solution that is oscillatory and/or decaying exponentially. Using it in the ODE gives a condition on the frequency of the damped oscillations,

Overdamped:If s is a real number, then the solution is simply a decaying exponential with no oscillation. This case occurs for , and is referred to as overdamped.

Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like . This case occurs for , and is referred to as underdamped. (The case where corresponds to the undamped simple harmonic oscillator, and in that case the solution looks like , as expected.)

Critically damped:The case where is the border between the overdamped and underdamped cases, and is referred to as critically damped. This turns out to be a desirable outcome in many cases where engineering design of a damped oscillator is required (e.g., a door closing mechanism).

Q factor and decay rate

The factors Q, damping ratio ζ, and exponential decay rate α are related such that

When a second-order system has

(that is, when the system is underdamped), it has two complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

poles that each have a real part of

; that is, the decay rate parameter

represents the rate of exponential decay of the oscillations. A lower damping ratio implies a lower decay rate, and so very underdamped systems oscillate for long times.
For example, a high quality tuning fork

Tuning fork

A tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs formed from a U-shaped bar of elastic metal . It resonates at a specific constant pitch when set vibrating by striking it against a surface or with an object, and emits a pure musical tone after waiting a...

, which has a very low damping ratio, has an oscillation that lasts a long time, decaying very slowly after being struck by a hammer.

Oscillation modes

Definition

Derivation

Q factor and decay rate

See also