Dunkl operator
Encyclopedia
In mathematics
, particularly the study of Lie groups, a Dunkl operator is a certain kind of mathematical operator, involving differential operator
s but also reflection
s in an underlying space.
Formally, let G be a Coxeter group
with reduced root system R and kv a multiplicity function on R (so ku = kv whenever the reflections σu and σv corresponding to the roots u and v are conjugate in G). Then, the Dunkl operator is defined by:
for 1 ≤ i ≤ N, x in RN, and f a smooth function on RN.
Dunkl operators were introduced by . One of Dunkl's major proofs was that Dunkl operators "commute," that is, they satisfy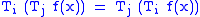
just as partial derivatives do. Thus Dunkl operators represent a meaningful generalization of partial derivatives.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly the study of Lie groups, a Dunkl operator is a certain kind of mathematical operator, involving differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s but also reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s in an underlying space.
Formally, let G be a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
with reduced root system R and kv a multiplicity function on R (so ku = kv whenever the reflections σu and σv corresponding to the roots u and v are conjugate in G). Then, the Dunkl operator is defined by:
for 1 ≤ i ≤ N, x in RN, and f a smooth function on RN.
Dunkl operators were introduced by . One of Dunkl's major proofs was that Dunkl operators "commute," that is, they satisfy
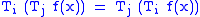just as partial derivatives do. Thus Dunkl operators represent a meaningful generalization of partial derivatives.