
Dvoretzky–Kiefer–Wolfowitz inequality
Encyclopedia
In the theory of probability
and statistics
, the Dvoretzky–Kiefer–Wolfowitz inequality predicts how close an empirically determined distribution function
will be to the distribution function
from which the empirical samples are drawn. It is named after Aryeh Dvoretzky
, Jack Kiefer
, and Jacob Wolfowitz
, who in 1956 proved
the inequality with a unspecified multiplicative constant C in front of the exponent on the right-hand side. In 1990, Pascal Massart proved the inequality with the sharp constant C = 1, confirming a conjecture due to Birnbaum and McCarty.
s with distribution function
F(·). Let Fn denote the associated empirical distribution function
defined by
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Dvoretzky–Kiefer–Wolfowitz inequality predicts how close an empirically determined distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
will be to the distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
from which the empirical samples are drawn. It is named after Aryeh Dvoretzky
Aryeh Dvoretzky
Aryeh Dvoretzky was a Russian-born Israeli mathematician, the winner of the 1973 Israel Prize in Mathematics. He is best known for his work in functional analysis, statistics and probability.-Biography:...
, Jack Kiefer
Jack Kiefer (mathematician)
Jack Carl Kiefer was an American statistician.- Biography :Jack Kiefer was born on January 25, 1924, in Cincinnati, Ohio, to Carl Jack Kiefer and Marguerite K. Rosenau...
, and Jacob Wolfowitz
Jacob Wolfowitz
Jacob Wolfowitz was a Polish-born American statistician and Shannon Award-winning information theorist. He was the father of former Deputy Secretary of Defense and World Bank Group President Paul Wolfowitz....
, who in 1956 proved
the inequality with a unspecified multiplicative constant C in front of the exponent on the right-hand side. In 1990, Pascal Massart proved the inequality with the sharp constant C = 1, confirming a conjecture due to Birnbaum and McCarty.
The DKW inequality
Given a natural number n, let X1, X2, …, Xn be real-valued independent and identically distributed random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F(·). Let Fn denote the associated empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
defined by
-
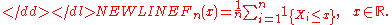
The Dvoretzky–Kiefer–Wolfowitz inequality bounds the probability that the random functionRandom functionA random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...
Fn differs from F by more than a given constant ε > 0 anywhere on the real line. More precisely, there is the one-sided estimate-

which also implies a two-sided estimate-

This strengthens the Glivenko–Cantelli theorem by quantifying the rate of convergenceRate of convergenceIn numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
as n tends to infinity. It also estimates the tail probability of the Kolmogorov–Smirnov statistic. The inequalities above follow from the case where F corresponds to be the uniform distributionUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on [0,1] in view of the fact
that Fn has the same distributions as Gn(F) where Gn is the empirical distribution of
U1, U2, …, Un where these are independendent and Uniform(0,1), and noting that-
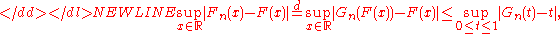
with equality if and only if F is continuous.
-
-
-

