Economic Lot Scheduling Problem
Encyclopedia
The Economic Lot Scheduling Problem (ELSP) is a problem in Operations management
that has been studied by a large number of researchers for over 50 years. The term was first used in 1958 by professor Jack Rogers
of Berkeley, who extended the economic order quantity
model to the case where there are several products to be produced on the same machine, so that one must decide both the lot size for each product and when each lot should be produced. The ELSP is a mathematical model of a common issue for almost any company or industry: planning what to manufacture, when to manufacture and how much to manufacture.
We assume a known, non-varying demand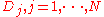
for the N products (for example, there might be N=3 products and customers require 7 items a day of Product 1, 5 items a day of Product 2 and 2 items a day of Product 3). Customer demand is met from inventory and the inventory is replenished by our production facility.
A single machine is available which can make all the products, but not in a perfectly interchangeable way. Instead the machine needs to be set up to produce one product, incurring a setup cost and/or setup time, after which it will produce this product at a known rate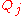
. When it is desired to produce a different product, the machine is stopped and another costly setup is required to begin producing the next product. Let 
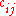be the setup cost when switching from product i to product j; and let 
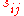be the setup time.
In addition, an inventory cost
is charged based on average inventory level of each item.
(To give a very concrete example, the machine might be a bottling machine and the products could be cases of bottled apple juice, orange juice and milk. The setup corresponds to the process of stopping the machine, cleaning it out and loading the tank of the machine with the desired fluid. This product switching must not be done too often or the setup costs will be large, but equally too long a production run of apple juice would be undesirable because it would lead to a large inventory cost for unsold cases of apple juice and perhaps stock-outs in orange juice and milk. The ELSP seeks the optimal tradeoff between these two extremes.)
The model is known as a NP hard problem since it is not currently possible to find the optimal solution without checking nearly every possibility. What has been done follows two approaches: restricting the solution to be of a specific type (which makes it possible to find the optimal solution for the narrower problem), or approximate solution of the full problem using heuristics or genetic algorithms.
Operations management
Operations management is an area of management concerned with overseeing, designing, and redesigning business operations in the production of goods and/or services. It involves the responsibility of ensuring that business operations are efficient in terms of using as little resources as needed, and...
that has been studied by a large number of researchers for over 50 years. The term was first used in 1958 by professor Jack Rogers
Jack Rogers
John Rogers was a footballer who played in The Football League for Aberdare Athletic, Sunderland and Norwich City . He also played for Crystal Palace.-References:...
of Berkeley, who extended the economic order quantity
Economic order quantity
Economic order quantity is the level of inventory that minimizes total inventory holding costs and ordering costs. It is one of the oldest classical production scheduling models. The framework used to determine this order quantity is also known as Wilson EOQ Model or Wilson Formula. The model was...
model to the case where there are several products to be produced on the same machine, so that one must decide both the lot size for each product and when each lot should be produced. The ELSP is a mathematical model of a common issue for almost any company or industry: planning what to manufacture, when to manufacture and how much to manufacture.
Model Formulation
The classic ELSP is concerned with scheduling the production of several products on a single machine in order to minimize the total costs incurred (which include setup costs and inventory holding costs).We assume a known, non-varying demand
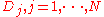for the N products (for example, there might be N=3 products and customers require 7 items a day of Product 1, 5 items a day of Product 2 and 2 items a day of Product 3). Customer demand is met from inventory and the inventory is replenished by our production facility.A single machine is available which can make all the products, but not in a perfectly interchangeable way. Instead the machine needs to be set up to produce one product, incurring a setup cost and/or setup time, after which it will produce this product at a known rate
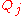. When it is desired to produce a different product, the machine is stopped and another costly setup is required to begin producing the next product. Let 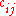be the setup cost when switching from product i to product j; and let 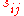be the setup time.In addition, an inventory cost
is charged based on average inventory level of each item.(To give a very concrete example, the machine might be a bottling machine and the products could be cases of bottled apple juice, orange juice and milk. The setup corresponds to the process of stopping the machine, cleaning it out and loading the tank of the machine with the desired fluid. This product switching must not be done too often or the setup costs will be large, but equally too long a production run of apple juice would be undesirable because it would lead to a large inventory cost for unsold cases of apple juice and perhaps stock-outs in orange juice and milk. The ELSP seeks the optimal tradeoff between these two extremes.)
Problem Status
The problem is well known in the Operations Research community, and a large body of academic research work has been created to improve the model and to create new variations that solve specific issues.The model is known as a NP hard problem since it is not currently possible to find the optimal solution without checking nearly every possibility. What has been done follows two approaches: restricting the solution to be of a specific type (which makes it possible to find the optimal solution for the narrower problem), or approximate solution of the full problem using heuristics or genetic algorithms.