
Edgeworth box
Encyclopedia
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, an Edgeworth box, named after Francis Ysidro Edgeworth
Francis Ysidro Edgeworth
Francis Ysidro Edgeworth FBA was an Irish philosopher and political economist who made significant contributions to the methods of statistics during the 1880s...
, is a way of representing various distributions of resources. Edgeworth made his presentation in his book Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences, 1881. Edgeworth's original two-axis depiction was developed into the now familiar box diagram by Pareto
Vilfredo Pareto
Vilfredo Federico Damaso Pareto , born Wilfried Fritz Pareto, was an Italian engineer, sociologist, economist, political scientist and philosopher. He made several important contributions to economics, particularly in the study of income distribution and in the analysis of individuals' choices....
in 1906 and was popularized in a later exposition by Bowley
Arthur Lyon Bowley
Sir Arthur Lyon Bowley was an English statistician and economist who worked on economic statistics and pioneered the use of sampling techniques in social surveys....
. The modern version of the diagram is commonly referred to as the Edgeworth–Bowley box.
The Edgeworth box is used frequently in general equilibrium theory. It can aid in representing
Representation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
the competitive equilibrium
Competitive equilibrium
Competitive market equilibrium is the traditional concept of economic equilibrium, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis...
of a simple system or a range of such outcomes that satisfy economic efficiency. It can also show the difficulty of moving to an efficient outcome in the presence of bilateral monopoly
Bilateral monopoly
In a bilateral monopoly there is both a monopoly and monopsony in the same market.In such, market price and output will be determined by forces like bargaining power of both buyer and seller...
. In the latter case, it serves as a precursor to the bargaining problem
Bargaining problem
The two person bargaining problem is a problem of understanding how two agents should cooperate when non-cooperation leads to Pareto-inefficient results. It is in essence an equilibrium selection problem; Many games have multiple equilibria with varying payoffs for each player, forcing the players...
of game theory that allows a unique numerical solution.
Example
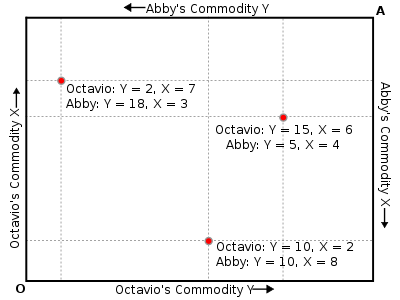
Imagine two people (Octavio and Abby) with a fixed amount of resources between the two of them — say, 10 liters of water and 20 hamburgers. If Abby takes 5 hamburgers and 4 liters of water, then Octavio is left with 15 hamburgers and 6 liters of water. The Edgeworth box is a rectangular diagram with Octavio's OriginOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
on one corner (represented by the O) and Abby's origin on the opposite corner (represented by the A). The width of the box is the total amount of one good, and the height is the total amount of the other good. Thus, every possible division of the goods between the two people can be represented as a point in the box.
Indifference curves (derived from each consumer's utility function) can be drawn in the box for both Abby and Octavio. The points on, for example, one of Octavio's indifference curves represent equally-liked combinations of quantities of the two goods. Hence Abby is indifferent between one combination of goods and another on any one of her indifference curves, and the same is true for Octavio. For example, Abby might value 1 liter of water and 13 hamburgers the same as 5 liters of water and 4 hamburgers, or 3 liters and 10 hamburgers. There are an infinite number of such curves that could be drawn among the combinations of goods for each consumer (Octavio or Abby).
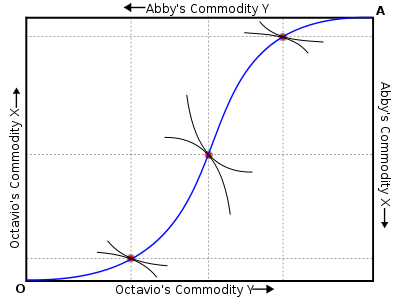
With Octavio's origin (the point representing zero of each good) at the lower left corner of the Edgeworth box and with Abby's origin at the upper right corner, typically Octavio's indifference curves would be convex to his origin and Abby's would be convex to her origin.
When an indifference curve for Abby crosses one of the indifference curves for Octavio at more than one point (so the two curves are not tangent to each other), a space in the shape of a lens is created by the crossing of the two curves; any point in the interior of this lens represents an allocation of the two goods between the two people such that both people would be better off, since the point is on an indifference curve farther from both of their respective origins.
Pareto set
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
at a single point), a combination of the two goods is identified that yields both consumers a level of utility that could not be improved for one person by a reallocation without decreasing the utility of the other person. Such a combination of goods is said to be Pareto optimal. The set of tangential points of contact between pairs of indifference curves, if all traced out, will form a trace connecting Octavio's origin (O) to Abby's (A). This curve connecting points O and A, which will not in general be a straight line, is called the Pareto set or the efficient locus, since each point on the curve is Pareto optimal.
The vocabulary used to describe different objects which are part of the Edgeworth box diverges. The entire Pareto set is sometimes called the contract curve
Contract curve
In microeconomics, the contract curve is the set of points, representing final allocations of two goods between two people, that could occur as a result of voluntary trading between those people given their initial allocations of the goods...
, while Mas-Colell
Andreu Mas-Colell
Andreu Mas-Colell is a Spanish economist, an expert in microeconomics and one of the world's leading mathematical economists. He is the founder of the Barcelona Graduate School of Economics and a professor in the department of economics at Pompeu Fabra University in Barcelona, Catalonia, Spain...
, Winston, and Green (1995) restrict the definition of the contract curve to only those points on the Pareto set which make both Abby and Octavio at least as well off as they are at their initial endowment. Other authors who have a more game theoretical
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
bent, such as Martin Osborne and Ariel Rubinstein
Ariel Rubinstein
Ariel Rubinstein is an Israeli economist who works in game theory. He was educated at the Hebrew University of Jerusalem, 1972–1979, in both mathematics and economics...
(1994), use the term core
Core (economics)
The core is the set of feasible allocations that cannot be improved upon by a subset of the economy's consumers. A coalition is said to improve upon or block a feasible allocation if the members of that coalition are better off under another feasible allocation that is identical to the first...
for the section of the Pareto set which is at least as good for each consumer as the initial endowment.
In order to calculate the Pareto set, the slope of the indifference curves for both consumers must be calculated at each point. That slope is the negative of the marginal rate of substitution
Marginal rate of substitution
In economics, the marginal rate of substitution is the rate at which a consumer is ready to give up one good in exchange for another good while maintaining the same level of utility.-Marginal rate of substitution as the slope of indifference curve:...
, so since the Pareto set is the set of points where both indifference curves are tangent, it is also the set of points where each consumer's marginal rate of substitution is equal to that of the other person.
See also
- Efficiency between production and consumption
- List of economics topics
- UtilityUtilityIn economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....

