
Edmonds's algorithm
Encyclopedia
In graph theory
, a branch of mathematics, Edmonds' algorithm or Chu–Liu/Edmonds' algorithm is an algorithm
for finding a maximum or minimum optimum branchings. When nodes are connected by weighted edges that are directed
, a minimum spanning tree
algorithm cannot be used. Instead an optimum branching algorithm should be applied using the algorithm proposed independently first by Yoeng-jin Chu and Tseng-hong Liu (1965) and then by Edmonds
(1967). To find a maximum path length, the largest edge value is found and connected between the two nodes, then the next largest value, and so on. If an edge creates a loop, it is erased. A minimum path length is found by starting from the smallest value.
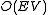 . There is a faster implementation of the algorithm by Robert Tarjan
. There is a faster implementation of the algorithm by Robert Tarjan
. The order is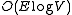 for a sparse graph and
for a sparse graph and 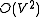 for a dense graph. This is as fast as Prim's algorithm
for a dense graph. This is as fast as Prim's algorithm
for an undirected minimum spanning tree. In 1986, Gabow, Galil, Spencer, and Tarjan made a faster implementation, and its order is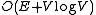 .
.
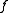 the function which, given a weighted directed graph
the function which, given a weighted directed graph 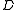 with a distinguished vertex
with a distinguished vertex  called the root, returns a spanning tree rooted at
called the root, returns a spanning tree rooted at  of minimal cost.
of minimal cost.
The precise description is as follows. Given a weighted directed graph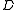 with root
with root  we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.
we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.
Now, for each node other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by
other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by 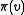 . If the marked edges form an SRT,
. If the marked edges form an SRT,  is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles
is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles 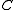 . We now define a weighted directed graph
. We now define a weighted directed graph 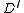 having a root
having a root 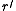 as follows. The nodes of
as follows. The nodes of 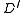 are the nodes of
are the nodes of 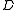 not in
not in 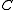 plus a new node denoted
plus a new node denoted 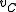 .
.
If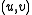 is an edge in
is an edge in  with
with 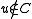 , include the edge
, include the edge  described below, in
described below, in 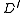 .
.
If ,
, 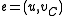 , and
, and 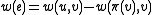 .
.
Otherwise, if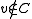 , let
, let 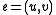 , and
, and 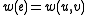 .
.
We include no other edges in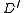 .
.
The root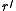 of
of 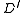 is simply the root
is simply the root  in
in 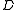 .
.
Using a call to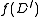 , find an SRT in
, find an SRT in 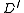 . Suppose in this SRT, the (unique) incoming edge at
. Suppose in this SRT, the (unique) incoming edge at 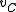 is
is 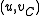 . This edge comes from some pair
. This edge comes from some pair 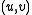 with
with 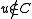 and
and 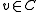 . Unmark
. Unmark 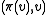 and mark
and mark 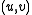 . Now the set of marked edges do form an SRT, which we define to be the value of
. Now the set of marked edges do form an SRT, which we define to be the value of 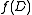 .
.
Observe that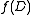 is defined in terms of
is defined in terms of 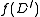 for weigthed directed rooted graphs
for weigthed directed rooted graphs 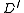 having strictly fewer vertices than
having strictly fewer vertices than 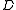 , and finding
, and finding 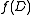 for a single-vertex graph is trivial.
for a single-vertex graph is trivial.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics, Edmonds' algorithm or Chu–Liu/Edmonds' algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for finding a maximum or minimum optimum branchings. When nodes are connected by weighted edges that are directed
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, a minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
algorithm cannot be used. Instead an optimum branching algorithm should be applied using the algorithm proposed independently first by Yoeng-jin Chu and Tseng-hong Liu (1965) and then by Edmonds
Jack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
(1967). To find a maximum path length, the largest edge value is found and connected between the two nodes, then the next largest value, and so on. If an edge creates a loop, it is erased. A minimum path length is found by starting from the smallest value.
Order
The order of this algorithm is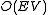 . There is a faster implementation of the algorithm by Robert Tarjan
. There is a faster implementation of the algorithm by Robert TarjanRobert Tarjan
Robert Endre Tarjan is a renowned American computer scientist. He is the discoverer of several important graph algorithms, including Tarjan's off-line least common ancestors algorithm, and co-inventor of both splay trees and Fibonacci heaps. Tarjan is currently the James S...
. The order is
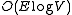 for a sparse graph and
for a sparse graph and 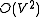 for a dense graph. This is as fast as Prim's algorithm
for a dense graph. This is as fast as Prim's algorithmPrim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
for an undirected minimum spanning tree. In 1986, Gabow, Galil, Spencer, and Tarjan made a faster implementation, and its order is
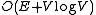 .
.Description
The algorithm has a conceptual recursive description. We will denote by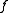 the function which, given a weighted directed graph
the function which, given a weighted directed graph 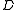 with a distinguished vertex
with a distinguished vertex  called the root, returns a spanning tree rooted at
called the root, returns a spanning tree rooted at  of minimal cost.
of minimal cost.The precise description is as follows. Given a weighted directed graph
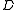 with root
with root  we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.
we first replace any set of parallel edges (edges between the same pair of vertices in the same direction) by a single edge with weight equal to the minimum of the weights of these parallel edges.Now, for each node
 other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by
other than the root, mark an (arbitrarily chosen) incoming edge of lowest cost. Denote the other endpoint of this edge by 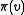 . If the marked edges form an SRT,
. If the marked edges form an SRT,  is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles
is defined to be this SRT. Otherwise, the set of marked edges form at least one cycle. Call (an arbitrarily chosen) one of these cycles 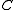 . We now define a weighted directed graph
. We now define a weighted directed graph 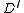 having a root
having a root 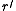 as follows. The nodes of
as follows. The nodes of 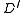 are the nodes of
are the nodes of 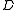 not in
not in 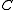 plus a new node denoted
plus a new node denoted 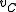 .
.If
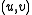 is an edge in
is an edge in  with
with 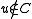 , include the edge
, include the edge  described below, in
described below, in 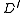 .
.If
 ,
, 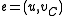 , and
, and 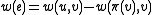 .
.Otherwise, if
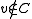 , let
, let 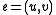 , and
, and 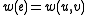 .
.We include no other edges in
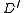 .
.The root
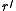 of
of 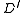 is simply the root
is simply the root  in
in 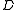 .
.Using a call to
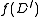 , find an SRT in
, find an SRT in 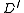 . Suppose in this SRT, the (unique) incoming edge at
. Suppose in this SRT, the (unique) incoming edge at 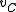 is
is 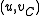 . This edge comes from some pair
. This edge comes from some pair 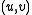 with
with 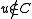 and
and 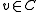 . Unmark
. Unmark 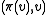 and mark
and mark 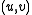 . Now the set of marked edges do form an SRT, which we define to be the value of
. Now the set of marked edges do form an SRT, which we define to be the value of 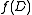 .
.Observe that
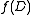 is defined in terms of
is defined in terms of 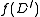 for weigthed directed rooted graphs
for weigthed directed rooted graphs 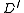 having strictly fewer vertices than
having strictly fewer vertices than 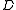 , and finding
, and finding 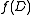 for a single-vertex graph is trivial.
for a single-vertex graph is trivial.Implementation
Let BV be a vertex bucket and BE be an edge bucket. Let v be a vertex and e be an edge of maximum positive weight that is incident to v. Ci is a circuit. G0 = (V0,E0) is the original digraph. ui is a replacement vertex for Ci.
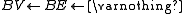
i=0
A:
if 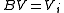 then goto B
then goto B
for some vertex 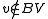 and
and 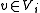 {
{
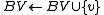
find an edge  such that w(e) = max{ w(y,v)|(y,v)
such that w(e) = max{ w(y,v)|(y,v)  Ei}
Ei}
if w(e) ≤ 0 then goto A
}
if 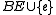 contains a circuit {
contains a circuit {
i=i+1
construct 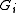 by shrinking
by shrinking 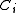 to
to 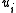
modify BE, BV and some edge weights
}
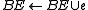
goto A
B:
while i ≠ 0 {
reconstruct 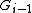 and rename some edges in BE
and rename some edges in BE
if 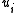 was a root of an out-tree in BE {
was a root of an out-tree in BE {
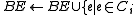 and
and 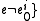
}else{
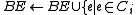 and
and 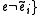
}
i=i-1
}
Maximum branching weight = 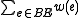
External links
- The Directed Minimum Spanning Tree Problem Description of the algorithm summarized by Shanchieh Jay Yang, May 2000.
- Edmonds's algorithm ( edmonds-alg ) – An open sourceOpen sourceThe term open source describes practices in production and development that promote access to the end product's source materials. Some consider open source a philosophy, others consider it a pragmatic methodology...
implementation of Edmonds's algorithm written in C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
and licensed under the MIT LicenseMIT LicenseThe MIT License is a free software license originating at the Massachusetts Institute of Technology . It is a permissive license, meaning that it permits reuse within proprietary software provided all copies of the licensed software include a copy of the MIT License terms...
. This source is using Tarjan's implementation for the dense graph. - AlgoWiki – Edmonds's algorithm - A public-domain implementation of Edmonds's algorithm written in JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
.

