
Minimum spanning tree
Encyclopedia
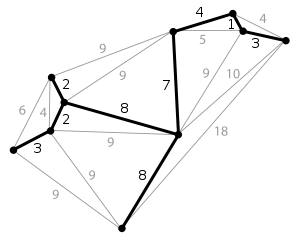
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of that graph is a subgraph that is a tree and connects all the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees for its connected components
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
.
One example would be a cable TV company laying cable to a new neighborhood. If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.
Possible multiplicity
There may be several minimum spanning trees of the same weight having a minimum number of edges; in particular, if all the edge weights of a given graph are the same, then every spanning tree of that graph is minimum.If there are n vertices in the graph, then each tree has n-1 edges.
Uniqueness
If each edge has a distinct weight then there will be only one, unique minimum spanning tree. This can be proved by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
or contradiction
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
. This is true in many realistic situations, such as the cable TV company example above, where it's unlikely any two paths have exactly the same cost. This generalizes to spanning forests as well.
A proof of uniqueness by contradiction is as follows.
- Say we have an algorithm that finds an MST (which we will call A) based on the structure of the graph and the order of the edges when ordered by weight. (Such algorithms do exist, see below.)
- Assume MST A is not unique.
- There is another spanning tree with equal weight, say MST B.
- Let e1 be an edge that is in A but not in B.
- As B is a MST, {e1}
 B must contain a cycle C.
B must contain a cycle C. - Then B should include at least one edge e2 that is not in A and lies on C.
- Assume the weight of e1 is less than that of e2.
- Replace e2 with e1 in B yields the spanning tree {e1}
 B - {e2} which has a smaller weight compared to B.
B - {e2} which has a smaller weight compared to B. - Contradiction. As we assumed B is a MST but it is not.
If the weight of e1 is larger than that of e2, a similar argument involving
tree {e2}
 A - {e1} also leads to a contradiction. Thus, we conclude that the assumption that there can be a second MST was false.
A - {e1} also leads to a contradiction. Thus, we conclude that the assumption that there can be a second MST was false.Minimum-cost subgraph
If the weights are positive, then a minimum spanning tree is in fact the minimum-cost subgraph connecting all vertices, since subgraphs containing cyclesPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
necessarily have more total weight.
Cycle property
For any cycle C in the graph, if the weight of an edge e of C is larger than the weights of other edges of C, then this edge cannot belong to an MST. Assuming the contrary, i.e. that e belongs to an MST T1, then deleting e will break T1 into two subtrees with the two ends of e in different subtrees. The remainder of C reconnects the subtrees, hence there is an edge f of C with ends in different subtrees, i.e., it reconnects the subtrees into a tree T2 with weight less than that of T1, because the weight of f is less than the weight of e.Cut property
For any cutCut (graph theory)
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.In an unweighted undirected graph, the...
C in the graph, if the weight of an edge e of C is smaller than the weights of all other edges of C, then this edge belongs to all MSTs of the graph. Indeed, assume the contrary
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, for example, edge BC (weighted 6) belongs to the MST T instead of edge e (weighted 4) in the left figure. Then adding e to T will produce a cycle, while replacing BC with e would produce MST of smaller weight.
Minimum-cost edge
If the edge of a graph with the minimum cost e is unique, then this edge is included in any MST. Indeed, if e was notincluded in the MST, removing any of the (larger cost) edges in the cycle formed after adding e to the MST, would yield a
spanning tree of smaller weight.
Algorithms
The first algorithm for finding a minimum spanning tree was developed by Czech scientist Otakar BorůvkaOtakar Boruvka
Otakar Borůvka was a Czech mathematician best known today for his work in graph theory, long before this was an established mathematical discipline....
in 1926 (see Borůvka's algorithm
Boruvka's algorithm
Borůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....
). Its purpose was an efficient electrical coverage of Moravia
Moravia
Moravia is a historical region in Central Europe in the east of the Czech Republic, and one of the former Czech lands, together with Bohemia and Silesia. It takes its name from the Morava River which rises in the northwest of the region...
. There are now two algorithms commonly used, Prim's algorithm
Prim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
and Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
. All three are greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
s that run in polynomial time, so the problem of finding such trees is in FP
FP (complexity)
In computational complexity theory, the complexity class FP is the set of function problems which can be solved by a deterministic Turing machine in polynomial time; it is the function problem version of the decision problem class P...
, and related decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s such as determining whether a particular edge is in the MST or determining if the minimum total weight exceeds a certain value are in P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
. Another greedy algorithm not as commonly used is the reverse-delete algorithm
Reverse-delete algorithm
The reverse-delete algorithm is an algorithm in graph theory used to obtain a minimum spanning tree from a given connected, edge-weighed graph. If the graph is disconnected, this algorithm will find a minimum spanning tree for each disconnected part of the graph...
, which is the reverse of Kruskal's algorithm.
If the edge weights are integers, then deterministic algorithms are known that solve the problem in O(m + n) integer operations. In a comparison model, in which the only allowed operations on edge weights are pairwise comparisons, found a linear time randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
based on a combination of Borůvka's algorithm and the reverse-delete algorithm. Whether the problem can be solved deterministically in linear time by a comparison-based algorithm remains an open question, however. The fastest non-randomized comparison-based algorithm, by
Bernard Chazelle
Bernard Chazelle
Bernard Chazelle is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he has found many of the best-known algorithms, such as linear-time triangulation of a simple polygon, as well as many useful complexity results, such...
, is based on the soft heap
Soft heap
In computer science, a soft heap is a variant on the simple heap data structure that has constant amortized time for 5 types of operations. This is achieved by carefully "corrupting" the keys of at most a certain fixed percentage of values in the heap...
,
an approximate priority queue.
Its running time is O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(m α(m,n)), where m is the number of edges, n is the number of vertices and α is the classical functional inverse of the Ackermann function. The function α grows extremely slowly, so that for all practical purposes it may be considered a constant no greater than 4; thus Chazelle's algorithm takes very close to linear time. Seth Pettie and Vijaya Ramachandran have found a provably optimal deterministic comparison-based minimum spanning tree algorithm, the computational complexity of which is unknown.
Research has also considered parallel algorithm
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
s for the minimum spanning tree problem.
With a linear number of processors it is possible to solve the problem in
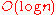 time.
time.demonstrate an algorithm that can compute MSTs 5 times faster on 8 processors than an optimized sequential algorithm. Typically, parallel algorithms are based on Borůvka algorithm—Prim's and especially Kruskal's algorithm do not scale as well to additional processors.
Other specialized algorithms have been designed for computing minimum spanning trees of a graph so large that most of it must be stored on disk at all times. These external storage algorithms, for example as described in "Engineering an External Memory Minimum Spanning Tree Algorithm" by Roman Dementiev et al., can operate, by authors' claims, as little as 2 to 5 times slower than a traditional in-memory algorithm. They rely on efficient external storage sorting algorithm
External sorting
External sorting is a term for a class of sorting algorithms that can handle massive amounts of data. External sorting is required when the data being sorted do not fit into the main memory of a computing device and instead they must reside in the slower external memory . External sorting...
s and on graph contraction techniques for reducing the graph's size efficiently.
The problem can also be approached in a distributed manner
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
. If each node is considered a computer and no node knows anything except its own connected links, one can still calculate the distributed minimum spanning tree
Distributed minimum spanning tree
The distributed minimum spanning tree problem involves the construction of a minimum spanning tree by a distributed algorithm, in a network where nodes communicate by message passing...
.
MST on complete graphs
Alan M. FriezeAlan M. Frieze
Alan M. Frieze is a professor in the Department of Mathematical Sciences at Carnegie Mellon University, Pittsburgh, United States. He graduated from the University of Oxford in 1966, and obtained his PhD from the University of London in 1975. His research interests lie in combinatorics, discrete...
showed that given a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on n vertices, with edge weights that are independent identically distributed random variables with distribution function
 satisfying
satisfying  , then as n approaches +∞
, then as n approaches +∞Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
the expected weight of the MST approaches
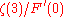 , where
, where  is the Riemann zeta function.
is the Riemann zeta function.Under the additional assumption of finite variance, Alan M. Frieze
Alan M. Frieze
Alan M. Frieze is a professor in the Department of Mathematical Sciences at Carnegie Mellon University, Pittsburgh, United States. He graduated from the University of Oxford in 1966, and obtained his PhD from the University of London in 1975. His research interests lie in combinatorics, discrete...
also proved convergence in probability. Subsequently, J. Michael Steele
J. Michael Steele
John Michael Steele is C.F. Koo Professor of Statistics at the Wharton School of the University of Pennsylvania, and he was previously affiliated with Stanford University, Columbia University and Princeton University....
showed that the variance assumption could be dropped.
In later work, Svante Janson
Svante Janson
Svante Janson is a Swedish mathematician. A member of the Royal Swedish Academy of Sciences since 1994, Janson has been the chaired professor of mathematics at Uppsala University since 1987....
proved a central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
for weight of the MST.
For uniform random weights in
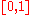 , the exact expected size of the minimum spanning tree has been computed for small complete graphs.
, the exact expected size of the minimum spanning tree has been computed for small complete graphs.| Vertices | Expected size | Approximative expected size |
|---|---|---|
| 2 | 1 / 2 | 0.5 |
| 3 | 3 / 4 | 0.75 |
| 4 | 31 / 35 | 0.8857143 |
| 5 | 893 / 924 | 0.9664502 |
| 6 | 278 / 273 | 1.0183151 |
| 7 | 30739 / 29172 | 1.053716 |
| 8 | 199462271 / 184848378 | 1.0790588 |
| 9 | 126510063932 / 115228853025 | 1.0979027 |
Related problems
A related problem is the k-minimum spanning treeK-minimum spanning tree
In mathematics, the K-minimum spanning tree is a graph G that spans some K of N vertices in the input set S with the minimum total length. K is less than or equal to N. The K-MST does not have to be a subgraph of the minimum spanning tree...
(k-MST), which is the tree that spans some subset of k vertices in the graph with minimum weight.
A set of k-smallest spanning trees is a subset of k spanning trees (out of all possible spanning trees) such that no spanning tree outside the subset has smaller weight. (Note that this problem is unrelated to the k-minimum spanning tree.)
The Euclidean minimum spanning tree
Euclidean minimum spanning tree
The Euclidean minimum spanning tree or EMST is a minimum spanning tree of a set of n points in the plane , where the weight of the edge between each pair of points is the distance between those two points...
is a spanning tree of a graph with edge weights corresponding to the Euclidean distance between vertices which are points in the plane (or space).
The rectilinear minimum spanning tree
Rectilinear minimum spanning tree
In graph theory, the rectilinear minimum spanning tree of a set of n points in the plane is a minimum spanning tree of that set, where the weight of the edge between each pair of points is the rectilinear distance between those two points.-Electronic design:The problem commonly arises in physical...
is a spanning tree of a graph with edge weights corresponding to the rectilinear distance between vertices which are points in the plane (or space).
In the distributed model
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
, where each node is considered a computer and no node knows anything except its own connected links, one can consider distributed minimum spanning tree
Distributed minimum spanning tree
The distributed minimum spanning tree problem involves the construction of a minimum spanning tree by a distributed algorithm, in a network where nodes communicate by message passing...
. Mathematical definition of the problem is the same but has different approaches for solution.
The capacitated minimum spanning tree
Capacitated minimum spanning tree
Capacitated minimum spanning tree is a minimal cost spanning tree of a graph that has a designated root node r and satisfies the capacity constraint c. The capacity constraint ensures that all subtrees incident on the root node r have no more than c nodes...
is a tree that has a marked node (origin, or root) and each of the subtrees attached to the node contains no more than a c nodes. c is called a tree capacity. Solving CMST optimally requires exponential time, but good heuristics such as Esau-Williams and Sharma produce solutions close to optimal in polynomial time.
The degree constrained minimun spanning tree is a minimun spanning tree in with each vertex is connected to no more than d other vertices, for some given number d. The case d = 2 is a special case of the traveling salesman problem, so the degree constrained minimum spanning tree is NP-hard in general.
For directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s, the minimum spanning tree problem is called the Arborescence
Arborescence (graph theory)
In graph theory, an arborescence is a directed graph in which, for a vertex u called the root and any other vertex v, there is exactly one directed path from u to v....
problem and can be solved in quadratic time using the Chu–Liu/Edmonds algorithm.
A maximum spanning tree is a spanning tree with weight greater than or equal to the weight of every other spanning tree.
Such a tree can be found with algorithms such as Prim's or Kruskal's after multiplying the edge weights by -1 and solving
the MST problem on the new graph. A path in the maximum spanning tree is the widest path
Widest path problem
In graph algorithms, the widest path problem, also known as the bottleneck shortest path problem or the maximum capacity path problem, is the problem of finding a path between two designated vertices in a weighted directed graph, maximizing the weight of the minimum-weight edge in the path.For...
in the graph between its two endpoints: among all possible paths, it maximizes the weight of the minimum-weight edge.
The dynamic MST problem concerns the update of a previously computed MST after an edge weight change in the original graph or the insertion/deletion of a vertex.
Minimum bottleneck spanning tree
A bottleneck edge is the highest weighted edge in a spanning tree.A spanning tree is a minimum bottleneck spanning tree (or MBST) if the graph does not contain a spanning tree with a smaller bottleneck edge weight.
A MST is necessarily a MBST (provable by the cut property), but a MBST is not necessarily a MST. If the bottleneck edge in a MBST is a bridge
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
in the graph, then all spanning trees are MBSTs.
See also
- Reverse-Delete algorithmReverse-delete algorithmThe reverse-delete algorithm is an algorithm in graph theory used to obtain a minimum spanning tree from a given connected, edge-weighed graph. If the graph is disconnected, this algorithm will find a minimum spanning tree for each disconnected part of the graph...
- Dijkstra's algorithmDijkstra's algorithmDijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
- Spanning tree protocolSpanning tree protocolThe Spanning Tree Protocol is a network protocol that ensures a loop-free topology for any bridged Ethernet local area network. The basic function of STP is to prevent bridge loops and ensuing broadcast radiation...
, used in switched networks - Minimum spanning tree-based image segmentationMinimum spanning tree-based segmentation-Image segmentation introduction:Image segmentation strives to partition a digital image into regions of pixels with similar properties, e.g. homogeneity. The higher-level region representation simplifies image analysis tasks such as counting objects or detecting changes, because region attributes...
- Edmonds's algorithmEdmonds's algorithmIn graph theory, a branch of mathematics, Edmonds' algorithm or Chu–Liu/Edmonds' algorithm is an algorithm for finding a maximum or minimum optimum branchings. When nodes are connected by weighted edges that are directed, a minimum spanning tree algorithm cannot be used...
- Distributed minimum spanning treeDistributed minimum spanning treeThe distributed minimum spanning tree problem involves the construction of a minimum spanning tree by a distributed algorithm, in a network where nodes communicate by message passing...
- Prim's algorithmPrim's algorithmIn computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
- Kruskal's algorithmKruskal's algorithmKruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
- Steiner treeSteiner treeThe Steiner tree problem, or the minimum Steiner tree problem, named after Jakob Steiner, is a problem in combinatorial optimization, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.The...
- Borůvka's algorithmBoruvka's algorithmBorůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....
Additional reading
.- Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová. (Section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's.)
- Thomas H. CormenThomas H. CormenThomas H. Cormen is the co-author of Introduction to Algorithms, along with Charles Leiserson, Ron Rivest, and Cliff Stein. He is a Full Professor of computer science at Dartmouth College and currently Chair of the Dartmouth College Department of Computer Science. Between 2004 and 2008 he directed...
, Charles E. LeisersonCharles E. LeisersonCharles Eric Leiserson is a computer scientist, specializing in the theory of parallel computing and distributed computing, and particularly practical applications thereof; as part of this effort, he developed the Cilk multithreaded language...
, Ronald L. Rivest, and Clifford SteinClifford SteinClifford Stein, a computer scientist, is currently a professor of industrial engineering and operations research at Columbia University in New York, NY, where he also holds an appointment in the Department of Computer Science. Stein is chair of the Industrial Engineering and Operations Research...
. Introduction to AlgorithmsIntroduction to AlgorithmsIntroduction to Algorithms is a book by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. It is used as the textbook for algorithms courses at many universities. It is also one of the most commonly cited references for algorithms in published papers, with over 4600...
, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp. 561–579. - Eisner, Jason (1997). State-of-the-art algorithms for minimum spanning trees: A tutorial discussion. Manuscript, University of Pennsylvania, April. 78 pp.
- Kromkowski, John David. "Still Unmelted after All These Years", in Annual Editions, Race and Ethnic Relations, 17/e (2009 McGraw Hill) (Using minimum spanning tree as method of demographic analysis of ethnic diversity across the United States).

