Euclidean minimum spanning tree - AbsoluteAstronomy.com

The Euclidean minimum spanning tree or EMST is a minimum spanning tree

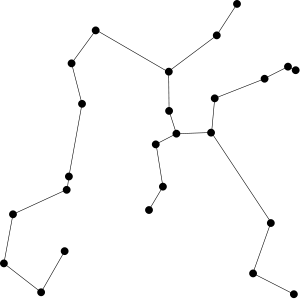
Minimum spanning tree

Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...

of a set of n points in the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

(or more generally in ℝ^d), where the weight of the edge between each pair of points is the distance between those two points. In simpler terms, an EMST connects a set of dots using lines such that the total length of all the lines is minimized and any dot can be reached from any other by following the lines.

In the plane, an EMST for a given set of points may be found in Θ

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

(n log n) time using O(n) space in the algebraic decision tree model of computation. Faster randomized algorithms of complexity O(n log log n) are known in more powerful models of computation that more accurately model the abilities of real computers.

In higher dimensions (d ≥ 3), finding an optimal algorithm remains an open problem

Open problem

In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...

Lower bound

An asymptotic lower bound of Ω

Big O notation

(n log n) for time complexity

Time complexity

In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...

of the EMST problem can be established in restricted models of computation, such as the algebraic decision tree and algebraic computation tree models, in which the algorithm has access to the input points only through certain restricted primitives that perform simple algebraic computations on their coordinates: in these models, the closest pair of points problem

Closest pair of points problem

The closest pair of points problem or closest pair problem is a problem of computational geometry: given n points in metric space, find a pair of points with the smallest distance between them...

requires Ω(n log n) time, but the closest pair is necessarily an edge of the EMST, so the EMST also requires this much time. However, if the input points have integer coordinates and bitwise operation

Bitwise operation

A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...

s and table indexing

Random access

In computer science, random access is the ability to access an element at an arbitrary position in a sequence in equal time, independent of sequence size. The position is arbitrary in the sense that it is unpredictable, thus the use of the term "random" in "random access"...

operations are permitted using those coordinates, then faster algorithms are possible.

Algorithms for computing EMSTs

The simplest algorithm to find an EMST, given n points, is to actually construct the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

on n vertices, which has n(n-1)/2 edges, compute each edge weight by finding the distance between each pair of points, and then run a standard minimum spanning tree algorithm (such as the version of Prim's algorithm

Prim's algorithm

In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...

or Kruskal's algorithm

Kruskal's algorithm

Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...

) on it. Since this graph has Θ(n²) edges for n distinct points, constructing it already requires Ω(n²) time. This solution also requires Ω(n²) space to store all the edges.

A better approach to finding the EMST in a plane is to note that it is a subgraph of every Delaunay triangulation

Delaunay triangulation

In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...

of the n points, a much-reduced set of edges:

Compute the Delaunay triangulation in O(n log n) time and O(n) space. Because the Delaunay triangulation is a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

, and there are no more than three times as many edges as vertices in any planar graph, this generates only O(n) edges.
Label each edge with its length.
Run a graph minimum spanning tree algorithm on this graph to find a minimum spanning tree. Since there are O(n) edges, this requires O(n log n) time using any of the standard minimum spanning tree algorithms such as Borůvka's algorithm
Boruvka's algorithm
Borůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....

, Prim's algorithm
Prim's algorithm
In computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...

, or Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...

.

The final result is an algorithm taking O(n log n) time and O(n) space.

If the input coordinates are integers and can be used as array indices, faster algorithms are possible: the Delaunay triangulation can be constructed by a randomized algorithm

Randomized algorithm

A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...

in O(n log log n) expected time. Additionally, since the Delaunay triangulation is a planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

, its minimum spanning tree can be found in linear time by a variant of Borůvka's algorithm that removes all but the cheapest edge between each pair of components after each stage of the algorithm. Therefore, the total expected time for this algorithm is O(n log log n).

Higher dimensions

The problem can also be generalized to n points in the d-dimensional space ℝ^d. In higher dimensions, the connectivity determined by the Delaunay triangulation (which, likewise, partitions the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

into d-dimensional simplices

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

) contains the minimum spanning tree; however, the triangulation might contain the complete graph. Therefore, finding the Euclidean minimum spanning tree as a spanning tree of the complete graph or as a spanning tree of the Delaunay triangulation both take O(dn²) time. For three dimensions it is possible to find the minimum spanning tree in time O((n log n)^4/3), and in any dimension greater than three it is possible to solve it in a time that is faster than the quadratic time bound for the complete graph and Delaunay triangulation algorithms. For uniformly random point sets it is possible to compute minimum spanning trees as quickly as sorting.

Subtree of Delaunay triangulation

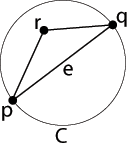
All edges of an EMST are edges of a relative neighborhood graph

Relative neighborhood graph

In computational geometry, the relative neighborhood graph is an undirected graph defined on a set of points in the Euclidean plane by connecting two points p and q by an edge whenever there does not exist a third point r that is closer to both p and q than they are to each other...

, which in turn are edges of a Gabriel graph

Gabriel graph

In mathematics, the Gabriel graph of a set S of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph with vertex set S in which any points P and Q in S are adjacent precisely if they are distinct and the closed disc of which line...

, which are edges in a Delaunay triangulation

Delaunay triangulation

of the points, as can be proven via the equivalent contrapositive statement: every edge not in a Delaunay triangulation is also not in any EMST. The proof is based on two properties of minimum spanning trees and Delaunay triangulations:

(the cycle property of minimum spanning trees): For any cycle C in the graph, if the weight of an edge e of C is larger than the weights of other edges of C, then this edge cannot belong to a MST.
(a property of Delaunay triangulations): If there is a circle with two of the input points on its boundary which contains no other input points, the line between those two points is an edge of every Delaunay triangulation.

Consider an edge e between two input points p and q which is not an edge of a Delaunay triangulation. Property 2 implies that the circle C with e as its diameter must contain some other point r inside. But then r is closer to both p and q than they are to each other, and so the edge from p to q is the longest edge in the cycle of points p → q → r → p, and by property 1 e is not in any EMST.

Expected size

The expected size of the EMST for large numbers of points has been determined by J. Michael Steele

J. Michael Steele

John Michael Steele is C.F. Koo Professor of Statistics at the Wharton School of the University of Pennsylvania, and he was previously affiliated with Stanford University, Columbia University and Princeton University....

. If

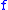is the density of the probability function for picking points, then for large

and

the size of the EMST is approximately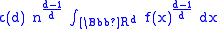

where

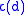is a constant depending only on the dimension

. The exact value of the constants are unknown but can be estimated from empirical evidence.

Applications

An obvious application of Euclidean minimum spanning trees is to find the cheapest network of wires or pipes to connect a set of places, assuming the links cost a fixed amount per unit length. However, while these give an absolute lower bound on the amount of connection needed, most such networks prefer a k-connected graph to a tree, so that failure of an any individual link will not split the network into parts.

Another application of EMSTs is a constant-factor approximation algorithm for approximately solving the Euclidean traveling salesman problem, the version of the traveling salesman problem on a set of points in the plane with edges labelled by their length. This realistic variation of the problem can be solved within a factor of 2 by computing the EMST, doing a walk along its boundary which outlines the entire tree, and then removing all but one occurrence of each vertex from this walk.

Planar realization

The realization problem for Euclidean minimum spanning trees is stated as follows: Given a tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

T = (V, E), find a location D(u) for each vertex u ∈ V so that T is a minimum spanning tree of D(u): u ∈ V, or determine that no such locations exist.
Testing of the existence of a realization in the plane is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.