Steiner tree - AbsoluteAstronomy.com

The Steiner tree problem, or the minimum Steiner tree problem, named after Jakob Steiner

Jakob Steiner

Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...

, is a problem in combinatorial optimization

Combinatorial optimization

In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...

, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.

The Steiner tree problem is superficially similar to the minimum spanning tree

Minimum spanning tree

Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...

problem: given a set V of points (vertices), interconnect them by a network (graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

) of shortest length, where the length is the sum of the lengths of all edges. The difference between the Steiner tree problem and the minimum spanning tree problem is that, in the Steiner tree problem, extra intermediate vertices and edges may be added to the graph in order to reduce the length of the spanning tree. These new vertices introduced to decrease the total length of connection are known as Steiner points or Steiner vertices. It has been proved that the resulting connection is a tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

, known as the Steiner tree. There may be several Steiner trees for a given set of initial vertices.

The Steiner tree problem has applications in circuit

Electrical network

An electrical network is an interconnection of electrical elements such as resistors, inductors, capacitors, transmission lines, voltage sources, current sources and switches. An electrical circuit is a special type of network, one that has a closed loop giving a return path for the current...

layout or network design. Most versions of the Steiner tree problem are NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

. In fact, one of these was among Karp's original 21 NP-complete problems

Karp's 21 NP-complete problems

One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...

. Some restricted cases can be solved in polynomial time. In practice, heuristics are used.

Euclidean Steiner tree

The original problem was stated in the form that has become known as the Euclidean Steiner tree problem or geometric Steiner tree problem: Given N points in the plane, the goal is to connect them by lines of minimum total length in such a way that any two points may be interconnected by line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

s either directly or via other points

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

and line segments.

It may be shown that the connecting line segments do not intersect each other except at the endpoints and form a tree, hence the name of the problem.

For the Euclidean Steiner problem, points added to the graph (Steiner points) must have a degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

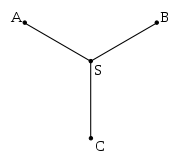
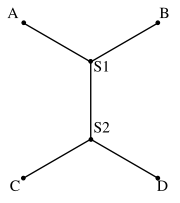
of three, and the three edges incident to such a point must form three 120 degree angles. It follows that the maximum number of Steiner points that a Steiner tree can have is N − 2, where N is the initial number of given points.

For N = 3, solution is given by a Steiner point located at the Fermat point

Fermat point

In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible...

of the triangle formed by the given points.

For general N, the Euclidean Steiner tree problem is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

, and hence it is not known whether an optimal solution

Optimization problem

In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...

can be found by using a polynomial-time algorithm. However, there is a polynomial-time approximation scheme

Polynomial-time approximation scheme

In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....

(PTAS) for Euclidean Steiner trees, i.e., a near-optimal solution can be found in polynomial time.

Rectilinear Steiner tree

The minimum rectilinear Steiner tree problem (MRST) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance

Euclidean distance

In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...

is replaced with the rectilinear distance. The problem arises in the physical design

Physical design (electronics)

In integrated circuit design, physical design is a step in the standard design cycle which follows after the circuit design. At this step, circuit representations of the components of the design are converted into geometric representations of shapes which, when manufactured in the corresponding...

of electronic design automation

Electronic design automation

Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...

. In VLSI circuits, wire routing is carried out by wires running only in vertical and horizontal directions, due to high computational complexity

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

of the task.

Generalization of minimum spanning tree

Steiner trees have also been studied in the context of weighted graphs. In the general Steiner tree problem (Steiner tree in graphs), we are given an edge-weighted graph G = (V, E, w) and a subset S ⊆ V of required vertices. A Steiner tree is a tree in G that spans all vertices of S. There are two versions of the problem: in the optimization problem

Optimization problem

associated with Steiner trees, the task is to find a minimum-weight Steiner tree; in the decision problem

Decision problem

In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...

, we are given a value k and the task is to determine whether a Steiner tree of total weight at most k exists. The decision problem was one of Karp's 21 NP-complete problems

Karp's 21 NP-complete problems

One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...

; hence the optimization problem is NP-hard

NP-hard

.

A special case of this problem is when G is a complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

, each vertex v ∈ V corresponds to a point in a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

, and the edge weights w(e) for each e ∈ E correspond to distances in the space. Put otherwise, the edge weights satisfy the triangle inequality

Triangle inequality

In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

. This variant is known as the metric Steiner tree problem. Given an instance of the (non-metric) Steiner tree problem, we can transform it in polynomial time into an equivalent instance of the metric Steiner tree problem; the transformation preserves the approximation factor.

While the Euclidean version admits a PTAS, it is known that the metric Steiner tree problem is APX-complete, i.e., it is believed that arbitrarily good approximation ratios cannot in general be achieved in polynomial time. There is a polynomial-time algorithm that finds a factor 1.55 approximation

Approximation algorithm

In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...

of a minimum Steiner tree.

In a special case of the graph problem, the Steiner tree problem for quasi-bipartite graph

Quasi-bipartite graph

In the mathematical field of graph theory, an instance of the Steiner tree problem is said to be quasi-bipartite if the non-terminal vertices in G form an independent set, i.e. if every edge is incident on at least one terminal...

s, S is required to include at least one endpoint of every edge in G.

The Steiner tree problem has also been investigated in higher dimensions and on various surfaces. Algorithms to find the Steiner minimal tree have been found on the sphere, torus, projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

, wide and narrow cones, and others.

Another generalizations of the Steiner tree problem are the k-edge-connected Steiner network problem and the k-vertex-connected Steiner network problem, where the goal is to find a k-edge-connected graph

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....

or a k-vertex-connected graph

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

rather than any connected graph.

Steiner ratio

A minimum spanning tree is a feasible but not usually optimal solution to the Steiner tree problem. The Steiner ratio is the largest possible ratio between the total length of a minimum spanning tree and the total length of a minimum Steiner tree.

In the metric Steiner tree problems, the Steiner ratio is 2. Therefore an algorithm that finds a minimum spanning tree is a polynomial-time factor-2 approximation algorithm

Approximation algorithm

for the metric Steiner tree problem.

In the Euclidean Steiner tree problem, the Steiner ratio is conjectured to be

. Despite earlier claims of a proof, the conjecture is still open.

External links

GeoSteiner (Steiner tree solver, Source available, for non commercial use)
http://www.archive.org/details/RonaldLG1988 (Movie: Ronald L Graham: The Shortest Network Problem (1988)
Fortran subroutine for finding the Steiner vertex of a triangle (i.e., Fermat point
Fermat point
In geometry the Fermat point of a triangle, also called Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible...

), its distances from the triangle vertices, and the relative vertex weights.
Phylomurka (Solver for the Steiner tree problem in networks)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.