
Reverse-delete algorithm
Encyclopedia
The reverse-delete algorithm is an algorithm
in graph theory
used to obtain a minimum spanning tree
from a given connected, edge-weighed graph. If the graph is disconnected, this algorithm will find a minimum spanning tree for each disconnected part of the graph. The set of these minimum spanning trees is called a minimum spanning forest, which contains every vertex in the graph.
This algorithm is a greedy algorithm
, choosing the best choice given any situation. It is the reverse of Kruskal's algorithm
, which is another greedy algorithm to find a minimum spanning tree. Kruskal’s algorithm starts with an empty graph and adds edges while the Reverse-Delete algorithm starts with the original graph and deletes edges from it. The algorithm works as follows:
2 sort E in decreasing order
3 Define an index i ← 0
4 while i < size(E)
5 Define edge temp ← E[i]
6 delete E[i]
7 if temp.v1 is not connected to temp.v2
8 E[i] ← temp
9 i ← i + 1
10 return edges[] E
In the above the graph is the set of edges E with each edge containing a weight and connected vertices v1 and v2.
Equally, the running time can be considered O(E log V (log log V)3) because the largest E can be is V2. Remember that logV2 = 2 * logV, so 2 is a multiplicative constant that will be ignored in big-O notation.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
used to obtain a minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
from a given connected, edge-weighed graph. If the graph is disconnected, this algorithm will find a minimum spanning tree for each disconnected part of the graph. The set of these minimum spanning trees is called a minimum spanning forest, which contains every vertex in the graph.
This algorithm is a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
, choosing the best choice given any situation. It is the reverse of Kruskal's algorithm
Kruskal's algorithm
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
, which is another greedy algorithm to find a minimum spanning tree. Kruskal’s algorithm starts with an empty graph and adds edges while the Reverse-Delete algorithm starts with the original graph and deletes edges from it. The algorithm works as follows:
- Start with graph G, which contains a list of edges E.
- Go through E in decreasing order of edge weights.
- For each edge, check if deleting the edge will further disconnect the graph.
- Perform any deletion that does not lead to additional disconnection.
Pseudocode
1 function ReverseDelete(edges[] E)2 sort E in decreasing order
3 Define an index i ← 0
4 while i < size(E)
5 Define edge temp ← E[i]
6 delete E[i]
7 if temp.v1 is not connected to temp.v2
8 E[i] ← temp
9 i ← i + 1
10 return edges[] E
In the above the graph is the set of edges E with each edge containing a weight and connected vertices v1 and v2.
Example
In the following example green edges are being evaluated by the algorithm and red edges have been deleted.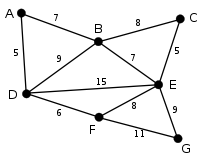 |
This is our original graph. The numbers near the edge indicate their edge weight. |
 |
The algorithm will start with the maximum weighted edge, which in this case is DE with an edge weight of 15. Since deleting edge DE does not further disconnect the graph it is deleted. |
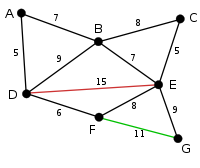 |
The next largest edge is FG so the algorithm will check if deleting this edge will further disconnect the graph. Since deleting the edge will not further disconnect the graph, the edge is then deleted. |
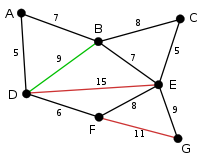 |
The next largest edge is edge BD so the algorithm will check this edge and delete the edge. |
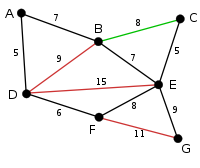 |
The next edge to check is edge EG, which will not be deleted since it would disconnect node G from the graph. Therefore, the next edge to delete is edge BC. |
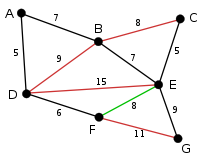 |
The next largest edge is edge EF so the algorithm will check this edge and delete the edge. |
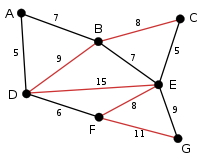 |
The algorithm will then search the remaining edges and will not find another edge to delete; therefore this is the final graph returned by the algorithm. |
Running time
The algorithm can be shown to run in O(E log E (log log E)3) time, where E is the number of edges and V is the number of vertices. This bound is achieved as follows:- sorting the edges by weight using a comparison sort in O(E log E) time
- E iterations of loop
- deleting in O(1) time
- connectivity checked in O(logV (log log V)3) time .
Equally, the running time can be considered O(E log V (log log V)3) because the largest E can be is V2. Remember that logV2 = 2 * logV, so 2 is a multiplicative constant that will be ignored in big-O notation.
See also
- Kruskal's algorithmKruskal's algorithmKruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
- Prim's algorithmPrim's algorithmIn computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized...
- Borůvka's algorithmBoruvka's algorithmBorůvka's algorithm is an algorithm for finding a minimum spanning tree in a graph for which all edge weights are distinct.It was first published in 1926 by Otakar Borůvka as a method of constructing an efficient electricity network for Moravia....
- Dijkstra's algorithmDijkstra's algorithmDijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...

