
Edmonds matrix
Encyclopedia
In graph theory
, the Edmonds matrix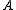 of a balanced bipartite graph
of a balanced bipartite graph
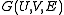 with sets of vertices
with sets of vertices 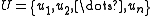 and
and 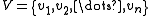 is defined by
is defined by
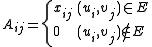
where the xij are indeterminates. One application of the Edmonds matrix of a bipartite graph is that the graph admits a perfect matching if and only if the polynomial det(Aij) in the xij is not identically zero. Furthermore, the number of perfect matchings is equal to the number of monomials in the polynomial det(A), and is also equal to the permanent
of A.
The Edmonds matrix is named after Jack Edmonds
. The Tutte matrix
is a generalisation to non-bipartite graphs.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Edmonds matrix
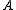 of a balanced bipartite graph
of a balanced bipartite graphBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
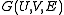 with sets of vertices
with sets of vertices 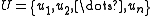 and
and 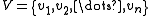 is defined by
is defined by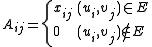
where the xij are indeterminates. One application of the Edmonds matrix of a bipartite graph is that the graph admits a perfect matching if and only if the polynomial det(Aij) in the xij is not identically zero. Furthermore, the number of perfect matchings is equal to the number of monomials in the polynomial det(A), and is also equal to the permanent
Permanent
The permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
of A.
The Edmonds matrix is named after Jack Edmonds
Jack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
. The Tutte matrix
Tutte matrix
In graph theory, the Tutte matrix A of a graph G = is a matrix used to determine the existence of a perfect matching: that is, a set of edges which is incident with each vertex exactly once....
is a generalisation to non-bipartite graphs.

