Effective potential
Encyclopedia
The effective potential, or effective potential energy is a mathematical expression combining the centrifugal potential energy with the potential energy
of a dynamical system
. Commonly used in calculating the orbit
s of planets (both Newtonian and relativistic
), the effective potential allows one to reduce a problem to fewer dimension
s. The units of the effective potential are kg m^2/s^2, the same as energy.
For example, consider a particle of mass m orbiting a much heavier object of mass M. Assuming Newtonian mechanics can be used, and the motion of the larger mass is negligible, then the conservation of energy
and angular momentum
give two constants E and L, with values
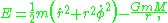
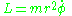
where
Only two variables are needed, since the motion occurs in a plane. Substituting the second expression into the first and rearranging gives
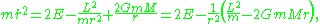
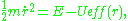
where
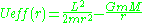
is the effective potentialA similar derivation may be found in José & Saletan, Classical Dynamics: A Contemporary Approach, pgs. 31–33. As is evident from the above equation, the original two variable problem has been reduced to a one variable problem. For many applications the effective potential can be treated exactly like the potential energy of a one-dimensional system: for instance, an energy diagram using the effective potential determines turning points and locations of stable and unstable equilibria
. A similar method may be used in other applications, for instance determining orbits in a general relativistic Schwarzschild metric
.
Effective potentials are widely used in various fields of condensed matter, like e.g. the Gauss-core potential (Likos 2002, Baeurle 2004) and the screened Coulomb potential (Likos 2001).
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
. Commonly used in calculating the orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s of planets (both Newtonian and relativistic
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
), the effective potential allows one to reduce a problem to fewer dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s. The units of the effective potential are kg m^2/s^2, the same as energy.
For example, consider a particle of mass m orbiting a much heavier object of mass M. Assuming Newtonian mechanics can be used, and the motion of the larger mass is negligible, then the conservation of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
give two constants E and L, with values
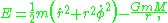
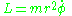
where
- r is the distance between the two masses,
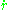is the derivative of r with respect to time,
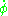is the angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of mass m, - G is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, - E is the total energy, and
- L is the angular momentum.
Only two variables are needed, since the motion occurs in a plane. Substituting the second expression into the first and rearranging gives
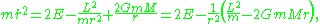
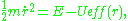
where
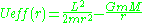
is the effective potentialA similar derivation may be found in José & Saletan, Classical Dynamics: A Contemporary Approach, pgs. 31–33. As is evident from the above equation, the original two variable problem has been reduced to a one variable problem. For many applications the effective potential can be treated exactly like the potential energy of a one-dimensional system: for instance, an energy diagram using the effective potential determines turning points and locations of stable and unstable equilibria
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
. A similar method may be used in other applications, for instance determining orbits in a general relativistic Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
.
Effective potentials are widely used in various fields of condensed matter, like e.g. the Gauss-core potential (Likos 2002, Baeurle 2004) and the screened Coulomb potential (Likos 2001).